8. Ολοκλήρωση

8.1. Διατύπωση του προβλήματος

Δίνεται μια συνάρτηση \(f(x)\), για την οποία θέλουμε να υπολογίσουμε το ολοκλήρωμά \(I\) στο διάστημα \([a,b]\). Αυτό μπορεί να γίνει αναλυτικά όταν γνωρίζουμε μία συνάρτηση \(F(x)\), για την οποία ισχύει:

\[\frac{dF(x)}{dx}=f(x)\]

οπότε:

\[I= \int_{a}^{b}f\left(x\right) dx = F(b)-F(a)\]

Exercise 8.1

Να υπολογιστεί αναλυτικά το ολοκλήρωμα της συνάρτησης \( f(x)=x^2 \) από 0 έως 10.

Solution to Exercise 8.1

\[F(x)=\frac{1}{3}x^3\]

\[I= \int_{0}^{10} x^2 dx = F(10)-F(0)=\frac{1}{3}10^3-0=\frac{1000}{3}\approx 333.33\]

Ωστόσο ορισμένες συναρτήσεις, όπως για παράδειγμα η συνάρτηση \({e^{-x^2}}\), δεν μπορούν να ολοκληρωθούν αναλυτικά, ενώ η λύση για άλλες μπορεί να είναι αρκετά δύσκολη. Τέλος σε ορισμένες περιπτώσεις δεν είναι διαθέσιμη η αναλυτική σχέση της συνάρτησης, αλλά πίνακες με τις τιμές της σε διακριτά σημεία.

Η αριθμητική ολοκλήρωση βασίζεται στην κατάτμηση του διαστήματος [a,b] σε μικρότερα επιμέρους διαστήματα, επομένως:

\[\begin{split} \begin{align} I&= \int_{a}^{b}f\left(x\right)=\\ &=\int_{x_0}^{x_{1}}f\left(x\right)dx+\int_{x_1}^{x_{2}}f\left(x\right)dx+\dots=\\ &=\sum_{i=0}^{n-1} \int_{x_i}^{x_{i+1}}f\left(x\right)dx \end{align} \end{split}\]

Τα όρια των επιμέρους διαστημάτων είτε είναι διαθέσιμα σε πίνακα, είτε προέρχονται από αναλυτικό υπολογισμό της \(f(x)\). Στην συνέχεια αρκεί η εφαρμογή απλοποιητικών παραδοχών, όπως τοπικές συναρτήσεις παρεμβολής, για την εξαγωγή των επιμέρους ολοκληρωμάτων.

8.2. Γραφική ολοκλήρωση

Σε μια γραφική αναπαράσταση το ολοκλήρωμα ισοδυναμεί με την επιφάνεια κάτω από την καμπύλη που ορίζει η συνάρτηση.

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(0, 10 + 1, 1)
y = x**2

fig, ax = plt.subplots()
ax.set(xlabel="x", ylabel="y")
ax.plot(x, y, "^-r")
ax.fill_between(x, 0, y)
ax.grid()

plt.show()

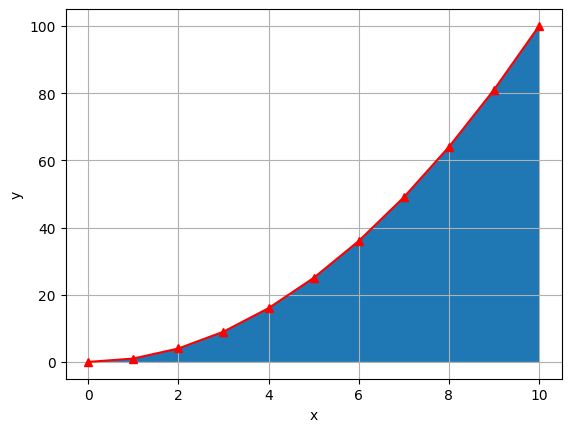
Exercise 8.2

Να λυθεί η Άσκηση 8.1 γραφικά.

Solution to Exercise 8.2

Για την γραφική ολοκλήρωση χρησιμοποιείται το καρτεσιανό πλέγμα (grid) στο γράφημα. Κάθε ορθογώνιο αντιπροσωπεύει \(2 \times 20=40\) μονάδες επιφάνειας.

Έχουμε 6 (σχεδόν) ολόκληρα ορθογώνια και 5 μισά άρα:

\[I \approx \left(6+5\frac{1}2\right) \times 40=340\]

8.3. Μέθοδος Riemann

Για να εφαρμόσουμε την μέθοδο Riemann, αρχικά χωρίζουμε το διάστημα ολοκλήρωσης σε \(n\) επιμέρους διαστήματα ανάμεσα στα \(n+1\) σημεία \(x_0,\dots,x_n\) (η αρίθμηση ξεκινάει από το 0 για λόγους συμβατότητας με την Python):

\[h_i=x_{i+1}-x_{i}\]

Αν θεωρήσουμε ότι αυτά τα διαστήματα έχουν το ίδιο πλάτος:

\[h=\frac{b-a}{n}\]

Σύμφωνα με τον δεξιό κανόνα του Riemann, θεωρούμε σταθερή τιμή \(f(x)=f(x_{i+1})\) στο διάστημα \([x_i,x_{i+1}]\). Γραφικά αυτό αντιπροσωπεύει ένα ορθογώνιο με ύψος που προκύπτει από την τιμή της \(f(x)\) στο δεξιό άκρο \(x_{i+1}\). Επομένως για κάθε διάστημα ισχύει:

\[\int_{x_i}^{x_{i+1}}f\left(x\right) dx \approx h f(x_{i+1})\]

και για το συνολικό ολοκλήρωμα:

\[Ι = h \sum_{i=0}^{n-1} f(x_{i+1})\]

Exercise 8.3

Να λυθεί η Άσκηση 8.1 αριθμητικά με τον δεξιό κανόνα του Riemann.

Solution to Exercise 8.3

Για \(n=10\) στο προηγούμενο παράδειγμα, προκύπτει \(h=1\):

\[\begin{split} \begin{align} x_0=a=0\\ x_1=x_0+h=1\\ \dots\\ x_i=x_{i-1}+h\\ \end{align} \end{split}\]

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(0, 10 + 1, 1)
y = x**2
yint = y[1:]  # Integrating with right y

fig, ax = plt.subplots()
ax.set(xlabel="x", ylabel="y")
ax.fill_between(x, 0, y)
ax.bar(x[:-1], height=yint, fill=False, width=1.0, align="edge", edgecolor="r")
# ax.grid()

plt.show()

integral_num = 1 * np.sum(yint)
integral_an = 1000 / 3
print("integral_num=", integral_num)
print(f"Rel_error={(integral_num - integral_an) / integral_an:.2%}")

integral_num= 385
Rel_error=15.50%

Tip

H συνάρτηση numpy.sum είναι βελτιστοποιημένη για αριθμητικούς υπολογισμούς πινάκων NumPy και παρέχει επιπλέον δυνατότητες από την sum της καθιερωμένης Python.

O κανόνας του Riemann μπορεί να εφαρμοστεί με την τιμή της \(f(x)\) στο αριστερό άκρο \(x_{i}\), δεξί άκρο \(x_{i+1}\) ή το μέσο \(\frac{x_{i}+x_{i+1}}{2}\).

Ερώτηση

Στο παράδειγμά μας η μέθοδος αυτή υπερεκτιμά το αποτέλεσμα. Πώς θα αλλάξει το σφάλμα:

• αν χρησιμοποιήσουμε την τιμή στο αριστερό άκρο ή το μέσο;

• αν η \(f(x)\) είναι γνησίως φθίνουσα;

• αν η \(f(x)\) είναι ημιτονοειδής;

• αν μειώσουμε το διάστημα \(h\);

Για την εκτίμηση της ακρίβειας της μεθόδου εφαρμόζεται η σειρά Taylor στην συνάρτηση \(f(x)\) (εδώ για τον αριστερό κανόνα):

\[f(x)=f(x_i)+\frac{f'(x_i)}{1!}(x-x_i)^1+\frac{f''(x_i)}{2!}(x-x_i)^2+\dots\]

Κάθε διάστημα υπολογίζεται προσεγγιστικά με αποκοπή του όρων της πρώτης παραγώγου και ανώτερων. Ο όρος της πρώτης παραγώγου μας δίνει την τάξη μεγέθους του σφάλματος:

\[\begin{split} \begin{align} \int_{x_{i}}^{x_{i+1}}f\left(x\right) dx &=& \int_{x_{i}}^{x_{i+1}}\left[f(x_i)+f^\prime(x_i)(x-x_i)+\dots\right] dx=\\ &=&\int_{x_{i}}^{x_{i+1}}\left[f(x_i)+\mathcal{O}(h)\right]dx \approx h f(x_i)+ \mathcal{O}(h^2) \end{align} \end{split}\]

Αν η ίδια διαδικασία εφαρμοστεί για το δεξιό άκρο, η τάξη του σφάλματος είναι παρόμοια:

\[\int_{x_{i}}^{x_{i+1}}f\left(x\right) dx \approx h f(x_{i+1})+ \mathcal{O}(h^2) \]

Το συνολικό ολοκλήρωμα και το σφάλμα του υπολογίζονται αθροίζοντας τα τμηματικά, επομένως:

\[\begin{split} \begin{align} I&= \int_{a}^{b}f\left(x\right) dx \approx \sum_{i=0}^{n-1} [h f(x_{i+1})+ \mathcal{O}(h^2)] \\ &= \sum_{i=0}^{n-1} h f(x_{i+1})+ \sum_{i=0}^{n-1} \mathcal{O}(h^2) = h \sum_{i=0}^{n-1} f(x_{i+1})+ n \mathcal{O}(h^2) \\ &= h \sum_{i=0}^{n-1} f(x_{i+1}) + \frac{b-a}{h} \mathcal{O}(h^2)=h \sum_{i=0}^{n-1} f(x_{i+1}) + \mathcal{O}(h) \end{align} \end{split}\]

8.4. Μέθοδος του τραπεζίου

Για καλύτερη ακρίβεια μπορούμε να αντικαταστήσουμε την σταθερή τιμή με μια γραμμική συνάρτηση παρεμβολής. Έτσι προκύπτει ένα τραπέζιο σχήμα για κάθε διάστημα. Για την εκτίμηση του σφάλματος μπορεί να χρησιμοποιηθεί ένα πολυώνυμο δευτέρου βαθμού. Ο τετραγωνικός όρος, ο οποίος αντιπροσωπεύει την τάξη μεγέθους τους σφάλματος, μετά την ολοκλήρωση έχει \(\mathcal{O}(h^3)\):

\[\int_{x_i}^{x_{i+1}}f\left(x\right) dx \approx h \frac{f(x_i)+f(x_{i+1})}2 + \mathcal{O}(h^3)\]

Η παραπάνω σχέση οδηγεί στην συνολική έκφραση για σταθερό διάστημα \(h\):

\[I= \int_{a}^{b}f\left(x\right) dx \approx \frac{h}{2}\left(f(x_0)+2\sum^{n-1}_{i=1} f(x_i)+ f(x_n)\right)+\mathcal{O}(h^2)\]

Η ακρίβεια της μεθόδου τραπεζίου είναι μια τάξη μεγέθους καλύτερη από την μέθοδο Riemann, δηλαδή \(\mathcal{O}(h^2)\) με σχεδόν ίδιο αριθμό πράξεων. Η συνάρτηση numpy.trapezoid και η ισοδύναμη scipy.integrate.trapezoid παρέχουν έτοιμες υλοποιήσεις της μεθόδου του τραπεζίου, οι οποίες είναι κατάλληλες και για ανομοιόμορφα διαστήματα \(h_i\).

Exercise 8.4

Να λυθεί η Άσκηση 8.1 αριθμητικά με την μέθοδο του τραπεζίου.

Solution to Exercise 8.4

import matplotlib.pyplot as plt
import numpy as np

h = 1
n = 10  #
n_points = n + 1
x = np.arange(0, n + h, h)
y = x**2

fig, ax = plt.subplots()
ax.set(xlabel="x", ylabel="y")
ax.fill_between(x, 0, y)
ax.plot(x, y, "-r", x, y * 0, "-r")
ax.bar(x, height=y, fill=False, width=0.0, align="edge", edgecolor="r")
# ax.grid()

plt.show()

I_sum = (h / 2) * (y[0] + 2 * np.sum(y[1 : n_points - 1]) + y[n_points - 1])
I_trapezoid = np.trapezoid(y, x)
I_analytical = 1000 / 3

print(f"Integral_sum={I_sum}")
print(f"Integral_numpy={I_trapezoid}")
print(f"Rel_error={(I_trapezoid - I_analytical) / I_analytical:.2%}")

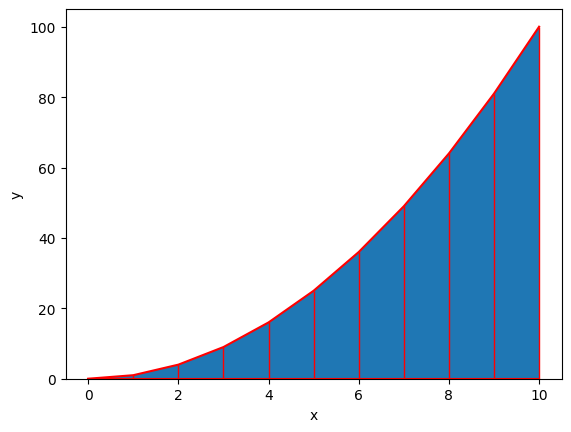
Integral_sum=335.0
Integral_numpy=335.0
Rel_error=0.50%

Exercise 8.5

Να υπολογιστεί με την μέθοδο του τραπεζίου το ολοκλήρωμα της \(\sin(x)\) στο διάστημα \([0,\pi]\) και να επαληθευθεί με την αναλυτική λύση.

Solution to Exercise 8.5

Η αναλυτική λύση είναι:

\[I=\int_0^{\pi}\sin(x)dx=\left[-\cos(x)\right]_0^{\pi}=-\cos(\pi)+\cos(0)=2\]

και η μέθοδος του τραπεζίου:

import numpy as np
from scipy.integrate import trapezoid

a = 0
b = np.pi
n = 11
x = np.linspace(a, b, n)
f = np.sin(x)

I_trapezoid = trapezoid(f, x)
I_analytical = -np.cos(np.pi) + np.cos(0)

print(f"Integral_numpy={I_trapezoid}")
print(f"Rel_error={(I_trapezoid - I_analytical) / I_analytical:.2%}")

Integral_numpy=1.9835235375094544
Rel_error=-0.82%

8.5. Κανόνες του Simpson

Η χρήση γραμμικών συναρτήσεων στην μέθοδο του τραπεζίου εισάγει σφάλματα που θα μπορούσαν να περιοριστούν με την χρήση καλύτερων συναρτήσεων παρεμβολής, όπως τα πολυώνυμα. Αυτή είναι η ιδέα πίσω από μια οικογένεια μεθόδων ολοκλήρωσης που ονομάζονται κανόνες του Simpson. Στον κανόνα 1/3 του Simpson, το πολυώνυμο είναι δευτέρου βαθμού, παίρνουμε 3 σημεία και υπολογίζουμε την ίδια συνάρτηση ανά δύο διαστήματα (\(2h\)):

\[\int_{x_i}^{x_{i+2}}f\left(x\right) dx \approx 2h \frac{f(x_i)+4f(x_{i+1})+f(x_{i+2})}6 + \mathcal{O}(h^5)\]

Το συνολικό άθροισμα στο διάστημα ολοκλήρωσης έχει τάξη σφάλματος \(\mathcal{O}(h^4)\).

Ιδανικά η μέθοδος εφαρμόζεται για άρτιο αριθμό διαστημάτων \(n\), αλλιώς πρέπει να γίνει ειδική διαχείριση στο πρώτο (\(h_0\)) ή στο τελευταίο διάστημα (\(h_n\)). Η συνάρτηση scipy.integrate.simpson αποτελεί υλοποίηση του κανόνα 1/3 του Simpson.

Στο κανόνα 3/8 του Simpson παρεμβάλουμε ένα πολυώνυμο τρίτου βαθμού σε διάστημα \(3h\) χρησιμοποιώντας 4 σημεία.

\[\int_{x_i}^{x_{i+3}}f\left(x\right) dx \approx 3h \frac{f(x_i)+3f(x_{i+1})+3f(x_{i+2})+f(x_{i+3})}8 + \mathcal{O}(h^5)\]

Ιδανικά η μέθοδος εφαρμόζεται για \(n\) πολλαπλάσιο του 3, αλλιώς πρέπει να γίνει ειδική διαχείριση στα πρώτα ή τα τελευταία διαστήματα. Επίσης μπορεί να χρησιμοποιηθεί σε συνδυασμό με τον κανόνα 1/3, αναλόγως το πλήθος των διαστημάτων. Ο κανόνας 1/3 του Simpson συναντάται συχνότερα από τον κανόνα 3/8, καθώς έχει την ίδια τάξη ακρίβειας με λιγότερα σημεία.

Exercise 8.6

Να λυθεί η Άσκηση 8.1 αριθμητικά με τον κανόνα 1/3 του simpson. Χρησιμοποιείστε την συνάρτηση scipy.integrate.simpson.

Solution to Exercise 8.6

from scipy.integrate import simpson
import numpy as np

x = np.arange(0, 10 + 1, 1)
y = x**2

I_simpson = simpson(y, x=x)
I_analytical = 1000 / 3

print(f"Integral_simpson={I_simpson}")
print(f"Relative_error={(I_simpson - I_analytical) / I_analytical:.2%}")

Integral_simpson=333.3333333333333
Relative_error=0.00%

Exercise 8.7

Να λυθεί η Άσκηση 8.5 αριθμητικά με τον κανόνα 1/3 του simpson. Χρησιμοποιείστε την συνάρτηση scipy.integrate.simpson.

Solution to Exercise 8.7

import numpy as np
from scipy.integrate import simpson

a = 0
b = np.pi
n = 11
x = np.linspace(a, b, n)
f = np.sin(x)

I_trapezoid = simpson(f, x=x)
I_analytical = 2.0

print(f"Integral_simpson={I_trapezoid}")
print(f"Rel_error={(I_trapezoid - I_analytical) / I_analytical:.2%}")

Integral_simpson=2.0001095173150043
Rel_error=0.01%

8.6. Ειδικές περιπτώσεις

Οι συναρτήσεις ολοκλήρωσης της SciPy μπορούν να χρησιμοποιηθούν για διπλά ολοκληρώματα ή και περισσότερων διαστάσεων.

Επίσης ιδιαίτερα χρήσιμες είναι οι συναρτήσεις της SciPy που δέχονται απευθείας συναρτήσεις \(f(x)\), αντί για σειρές σημείων, όπως η scipy.integrate.quad. Σε αυτή την περίπτωση δηλώνεται η συνάρτηση που θα ολοκληρωθεί και τα όρια της ολοκλήρωσης και αποφασίζει η quad ποια μέθοδο θα χρησιμοποιήσει και πόσα σημεία χρησιμοποιώντας την βιβλιοθήκη QUADPACK[10]. H quad επιστρέφει μαζί με το αποτέλεσμα και μια εκτίμηση του απόλυτου σφάλματος.

Exercise 8.8

Να λυθεί η Άσκηση 8.5 αριθμητικά με την συνάρτηση scipy.integrate.quad.

Solution to Exercise 8.8

from scipy.integrate import quad
import numpy as np


def f(x: float) -> float:
    return np.sin(x)


I_quad, err = quad(f, 0, np.pi)
I_analytical = 2.0

print(f"Integral_numerical={I_quad}")
print(f"Absolute_error={err:g}")
print(f"Relative_error={(I_quad - I_analytical) / I_analytical:g}")

Integral_numerical=2.0
Absolute_error=2.22045e-14
Relative_error=0