10. Προβλήματα αρχικής τιμής

10.1. Διατύπωση του προβλήματος

Στην φυσική και σε άλλες επιστήμες συναντάμε συχνά προβλήματα αρχικής τιμής, προβλήματα δηλαδή στα οποία είναι γνωστή μια αρχική κατάσταση και η διαφορική εξίσωση περιγράφει την μεταβολή της κατάστασης. Η ανεξάρτητη μεταβλητή είναι συνήθως ο χρόνος, χωρίς αυτό να είναι δεσμευτικό για τις μεθόδους που θα περιγραφούν παρακάτω.

Με δεδομένη λοιπόν την διαφορική εξίσωση

\[ y'=f(t,y(t)) \]

και μια αρχική κατάσταση \(y(t_0)\), θα υπολογίσουμε την εξέλιξη της συνάρτησης \(y(t)\).

Exercise 10.1

Το μεταβατικό ισοζύγιο ενέργειας του τοιχώματος ενός μεταλλικού μαγειρικού σκεύους δίνεται από την σχέση:

\[ m C_p \frac{dT}{dt}=-hA(T-T_a)\]

ή ισοδύναμα

\[ \frac{dT}{dt}=-\frac{1}{τ}(T-T_a) \]

όπου \(τ=\frac{mC_p}{hA}\), η σταθερά του χρόνου.

Η εξίσωση αυτή έχει προκύψει με την παραδοχή ότι η εξωτερική θερμική αντίσταση είναι αρκετά μεγαλύτερη από την εσωτερική ή ισοδύναμα ότι το σκεύος έχει ομοιόμορφη θερμοκρασία \(T\) σε όλο το πάχος του.

Αν η αρχική θερμοκρασία του σκεύους στον χρόνο \(0\text{s}\) είναι \(100\text{°C}\), η θερμοκρασία του αέρα σταθερή στους \(20\text{°C}\) και η σταθερά του χρόνου \(τ=41.8\text{s}\), υπολογίστε την εξέλιξη της θερμοκρασίας για \(100\text{s}\) και την χρονική στιγμή που θα η θερμοκρασία του σκεύους θα φτάσει στους 40°C.

Solution to Exercise 10.1

H ανεξάρτητη μεταβλητή είναι ο χρόνος \(t\) και η εξαρτημένη η θερμοκρασία \(Τ\).

Η περιοχή της επίλυσης για τον χρόνο \(t\) είναι το πεδίο \([0,100]\).

Γνωστή είναι η η θερμοκρασία στον χρόνο μηδέν, δηλαδή \(T(0)=T_0\).

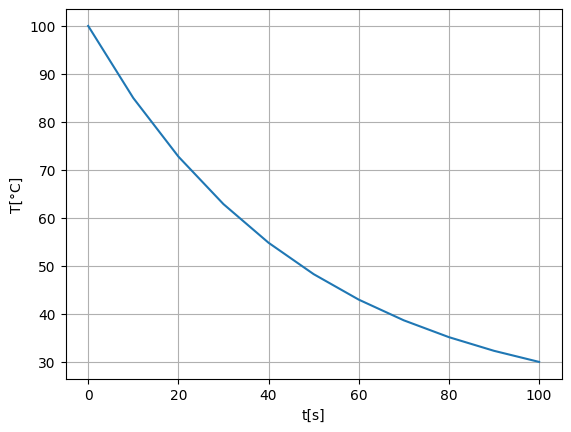
Η αναλυτική επίλυση είναι αρκετά απλή σε αυτό το πρόβλημα. Με μια απλή αναδιάταξη:

\[\frac{dT}{T-T_a}=-\frac{dt}{τ}\]

Ολοκληρώνοντας και τις δύο πλευρές της εξίσωσης:

\[\int_{T_0}^T\frac{dT}{T-T_a}=\int_0^t-\frac{dt}{τ}\]

και τελικά

\[Τ=T_a+(T_0-Τ_a)e^{-\frac{t}{τ}}\]

Η γραφική αναπαράσταση της λύσης είναι:

import numpy as np
import matplotlib.pyplot as plt

dt = 10  # s
tau = 48.1  # s
Ta = 20  # °C
T0 = 100  # °C
n = 10

t = np.arange(0, (n + 1) * dt, dt)
Tan = Ta + (T0 - Ta) * np.exp(-t / tau)

fig, ax = plt.subplots()
ax.set(xlabel="t[s]", ylabel="T[°C]")
ax.plot(t, Tan, "-")
ax.grid()

plt.show()

Στην αριθμητική ολοκλήρωση ξεκινάμε από την αρχική κατάσταση και εκτελούμε διαδοχικά βήματα \(h=Δt\). Σε κάθε βήμα είναι γνωστή η κατάσταση \(y(t_i)\) και υπολογίζεται προσεγγιστικά η καινούργια κατάσταση \((y(t_{i+1})\). Η διαδικασία αυτή εφαρμόζεται επαναληπτικά για το διάστημα που επιθυμούμε. Για τον υπολογισμό της καινούργιας κατάστασης είναι απαραίτητη η χρήση παραδοχών, η επιλογή των οποίων χαρακτηρίζει τις μεθόδους που θα συζητηθούν παρακάτω.

10.2. Μέθοδος Euler

Η πιο απλή προσέγγιση είναι να θεωρήσουμε σταθερή παράγωγο κατά την μεταβολή της ανεξάρτητης μεταβλητής από το \(t_{i}\) σε \(t_{i+1}\). Έτσι μπορεί να υπολογιστεί η καινούργια κατάσταση ως:

\[y_{t_{i+1}}=y_{t_{i}}+y'(t_{i+1}-t_i)\]

Για τον υπολογισμό της παραγώγου \(y'\) μπορεί να επιλεγεί το σημείο \(t_i\), το \(t_{i+1}\) ή κάποια άλλη προσέγγιση. Αναλόγως την επιλογή, προκύπτουν οι παρακάτω βασικές παραλλαγές της μεθόδου Euler.

10.2.1. Ρητή μέθοδος

Στην ρητή ή προς τα εμπρός μέθοδο, η σταθερή παράγωγος υπολογίζεται στην αρχή του βήματος, δηλαδή στο \(t_i\).

\[y'=f\left(t_i,y(t_i)\right)\]

Καθώς το \(y_{t_i}\) είναι ήδη γνωστό, μπορεί να εφαρμοστεί η σχέση απευθείας, από το οποίο προέρχεται και το όνομα της μεθόδου.

Exercise 10.2

Επιλύστε την Άσκηση 10.1 με την ρητή μέθοδο και βήμα \(\Delta t=10\text{s}\). Συγκρίνετε γραφικά τα αποτελέσματα με την αναλυτική λύση.

Solution to Exercise 10.2

from IPython.display import HTML
import matplotlib.animation
import matplotlib.pyplot as plt
import numpy as np

dt = 10  # s
tmax = 100  # s
tau = 48.1  # s
Ta = 20  # °C
T0 = 100  # °C

t = np.arange(0.0, tmax + dt, dt)
Tan = Ta + (T0 - Ta) * np.exp(-t / tau)

Texp = np.empty(t.size)
Texp[0] = T0
for i in range(t.size - 1):
    dydt = -1 / tau * (Texp[i] - Ta)
    Texp[i + 1] = Texp[i] + dydt * dt


fig, ax = plt.subplots()
ax.set(xlabel="t[s]", ylabel="T[°C]")
ax.grid()
margin = 5
ax.set_xlim(0 - margin, 100 + margin)
ax.set_ylim(30 - margin, 100 + margin)
(l1,) = ax.plot([], [], "-", label="Analytical")
(l2,) = ax.plot([], [], "-", label="Explicit")
(p2,) = ax.plot([], [], "or")


def animate(n):
    l1.set_data(t[: n + 1], Tan[: n + 1])
    l2.set_data(t[: n + 1], Texp[: n + 1])
    p2.set_data(t[n : n + 1], Texp[n : n + 1])
    # print(n)


ani = matplotlib.animation.FuncAnimation(fig, animate, frames=t.size)
plt.close()
HTML(ani.to_jshtml())

Once Loop Reflect

Παρατηρούμε ότι το σφάλμα μεγαλώνει καθώς απομακρυνόμαστε από την αρχική κατάσταση. Η ρητή μέθοδος είναι εύκολη στη εφαρμογή, αλλά μπορεί να έχει προβλήματα ευστάθειας αν το βήμα δεν είναι επαρκώς μικρό. Το σφάλμα σε κάθε βήμα της ρητής μεθόδου είναι \(\mathcal{O}(h^2)\) και το συνολικό σφάλμα στο τέλος της ολοκλήρωσης \(\mathcal{O}(h)\).

10.2.2. Άρρητη μέθοδος

Στην αρρητή ή πεπλεγμένη ή προς τα πίσω μέθοδο, η σταθερή παράγωγος \(y'\) υπολογίζεται στο τέλος του βήματος (\(t_{i+1}\)), δηλαδή

\[y'=f\left(t_{i+1},y(t_{i+1})\right)\]

και επομένως πρέπει να λυθεί αλγεβρικά η (άρρητη) εξίσωση:

\[y_{i+1}=y_{i}+f\left(t_{i+1},y(t_{i+1})\right)(t_{i+1}-t_i)\]

Exercise 10.3

Επιλύστε την Άσκηση 10.1 με την αρρητή μέθοδο και βήμα Δt=10s. Συγκρίνετε γραφικά τα αποτελέσματα με την αναλυτική λύση και την ρητή μέθοδο.

Solution to Exercise 10.3

\[T_{i+1}=T_{i}+\left(-\frac{T_{i+1}-T_a}{τ}\right)Δt \]

\[T_{i+1}=\frac{T_i+\frac{Δt}{τ}T_a}{1+\frac{Δt}{τ}}\]

import numpy as np
import matplotlib.pyplot as plt

dt = 10  # s
tau = 48.1  # s
Ta = 20  # °C
T0 = 100  # °C
n = 10

Texp = np.empty(n + 1)
Timp = np.empty(n + 1)
t = np.empty(n + 1)

Texp[0] = T0
Timp[0] = T0
t[0] = 0.0
for i in range(n):
    dydx = -1 / tau * (Texp[i] - Ta)
    Texp[i + 1] = Texp[i] + dydx * dt
    Timp[i + 1] = (Timp[i] + dt / tau * Ta) / (1 + dt / tau)
    t[i + 1] = t[i] + dt

fig, ax = plt.subplots()
ax.set(xlabel="t[s]", ylabel="T[°C]")
ax.plot(t, Ta + (T0 - Ta) * np.exp(-t / tau), "-", label="Analytical")
ax.plot(t, Texp, "--o", label="Explicit")
ax.plot(t, Timp, "--*", label="Implicit")
ax.legend()
ax.grid()

plt.show()

Λόγω της απαιτούμενης αλγεβρικής επίλυσης, η άρρητη μέθοδος είναι πιο δύσκολη στην εφαρμογή και γι’ αυτό συνήθως δεν είναι η πρώτη επιλογή σε μία αρχική επίλυση. Έχει όμως το πλεονέκτημα της ευστάθειας χωρίς συνθήκες, που σημαίνει ότι μπορεί να χρησιμοποιηθεί σε απλές και δύσκαμπτες διαφορικές εξισώσεις. Επίσης συγκλίνει με μεγαλύτερα χρονικά βήματα από την ρητή μέθοδο. Σε κάθε περίπτωση ο έλεγχος της ακρίβειας των αποτελεσμάτων είναι απαραίτητος.

10.2.3. Τραπεζοειδής κανόνας Euler

Στην μέθοδο τραπεζοειδούς κανόνα για διαφορικές εξισώσεις ή Crank-Nicholson ή ημιπεπλεγμένη μέθοδο, επιλέγουμε την μέση τιμή των παραγώγων στο \(i\) και \(i+1\).

\[y'=\frac{f(t_{i},y(t_{i}))+f(t_{i+1},y(t_{i+1}))}{2}\]

Η μέθοδος αυτή έχει καλύτερη ακρίβεια από τις δύο προηγούμενες με ελαφρώς μεγαλύτερη δυσκολία στην αλγεβρική επίλυση από την αρρητή μέθοδο.

10.3. Μέθοδοι Runge-Kutta

Για την ολοκλήρωση κανονικών διαφορικών εξισώσεων με καλύτερη ακρίβεια μπορούμε να χρησιμοποιήσουμε περισσότερες από μία εκτιμήσεις της κλίσης εντός ενός βήματος. Οι μέθοδοι που στηρίζονται σε αυτή την προσέγγιση ανήκουν στην οικογένεια μεθόδων Runge-Kutta. Η πιο γνωστή από αυτές είναι η κλασσική μέθοδος Runge-Kutta τέταρτης τάξης (RK4), η οποία έχει τοπικό σφάλμα αποκοπής \(\mathcal{O}(h^4)\) και βασίζεται στον υπολογισμό 4 εκτιμήσεων της κλίσης όπως παρακάτω:

\[\begin{split} \begin{aligned} k_1&=F\left(t_j,y(t_j)\right)\\ k_2&=F\left(t_j+\frac{h}2,y(t_j)+\frac{1}2k_1h\right)\\ k_3&=F\left(t_j+\frac{h}2,y(t_j)+\frac{1}2k_2h\right)\\ k_4&=F\left(t_j+h,y(t_j)+k_3h\right)\\ \\ y(t_{j+1})&=y(t_{j})+\frac{h}6\left(k_1+2k_2+2k_3+k4\right) \end{aligned} \end{split}\]

Σημειώνεται ότι μπορούν να προκύψουν άπειρες παραλλαγές με ακρίβεια την ίδιας τάξης. Για την περιγραφή των διαφορετικών μεθόδων Runge-Kutta χρησιμοποιείται ο πίνακας Butcher, ο οποίος περιλαμβάνει:

• τους συντελεστές \(a\) για τον υπολογισμό των κλίσεων \(k\) σε όλα τα βήματα (1 έως \(s\)) της μεθόδου,

• τους συντελεστές \(c\) για τον υπολογισμό των χρονικών στιγμών \(t\) των κλίσεων,

• και τους συντελεστές \(b\) για τον υπολογισμό της καινούργιας κατάστασης \(y(t_{j+1})\) από τις κλίσεις \(k\).

\[\begin{split} \begin{array}{c|ccccc} 0 & \\ c_2 & a_{21} & \\ c_3 & a_{31} & a_{32} & \\ \vdots & \vdots & & \ddots \\ c_s & a_{s_1} & a_{s2} & \cdots & a_{s,s-1} \\ \hline & b_1 & b_2 & \cdots & b_{s-1} & b_s \end{array} \end{split}\]

Για παράδειγμα στην κλασσική μέθοδο Runge-Kutta, ο πίνακας Butcher είναι:

\[\begin{split} \begin{array}{c|ccccc} 0 & \\ \frac{1}2 & \frac{1}2 & \\ \frac{1}2 & 0 & \frac{1}2 & \\ 1 & 0 & 0 & 1 & \\ \hline & \frac{1}6 & \frac{2}6 & \frac{2}6 & \frac{1}6 \end{array} \end{split}\]

10.4. Μέθοδοι μεταβλητού βήματος

Οι μέθοδοι αρχικής τιμής μπορούν να επιταχυνθούν σημαντικά αν επιλεγεί μικρό χρονικό βήμα στις περιοχές που η παράγωγος μεταβάλλεται απότομα και μεγαλύτερο στις περιοχές που μεταβάλλεται ομαλά. Για την αυτόματη προσαρμογή του χρονικού βήματος έχουν αναπτυχθεί μέθοδοι που στηρίζονται στην εκτίμηση της καινούργιας κατάστασης με δύο υπολογισμούς Runge-Kutta διαφορετικής ακρίβειας. Η διαφορά τους δίνει μια εκτίμηση του σφάλματος και έτσι μπορεί να επιλεγεί αυτόματα ένα βήμα που ικανοποιεί τις απαιτήσεις ακρίβειας που θέτουμε. Η πιο συνηθισμένη μέθοδος μεταβλητού βήματος είναι η Dormand-Prince. Συγκριμένα χρησιμοποιείται στην συνάρτηση ομπρέλα solve_ivp της μονάδας κώδικα SciPy για προβλήματα αρχικής τιμής. Αποτελεί μάλιστα συστατικό της προεπιλεγμένης μεθόδου RK45), η οποία περιλαμβάνει δύο υπολογισμούς Runge-Kutta με ακρίβεια 4ης και 5ης τάξης για τον αυτόματο έλεγχο του χρονικού βήματος. Για την περίπτωση που θέλουμε να πάρουμε τιμές κατάστασης σε δεδομένες χρονικές στιγμές διατίθεται το προαιρετικό όρισμα t_eval, το οποίο αναγκάζει την solve_ivp να κάνει πολυωνυμική παρεμβολή.

Exercise 10.4

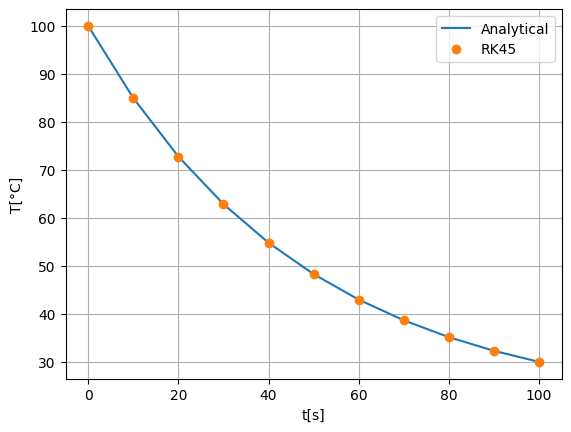
Επιλύστε την Άσκηση 10.1 με την μέθοδο RK45 της συνάρτησης scipy.integrate.solve_ivp και εξάγετε τα αποτελέσματα με βήμα Δt=10s. Συγκρίνετε γραφικά τα αποτελέσματα με την αναλυτική λύση.

Solution to Exercise 10.4

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

dt = 10  # s
tau = 48.1  # s
Ta = 20.0  # °C
T0 = 100.0  # °C

t = np.arange(0.0, 100.0 + dt / 2, dt)


def dTdt(t: float, T: float) -> float:
    return (Ta - T) / tau


sol = solve_ivp(dTdt, (0, 100), [T0], t_eval=t)

fig, ax = plt.subplots()
ax.set(xlabel="t[s]", ylabel="T[°C]")
ax.plot(t, Ta + (T0 - Ta) * np.exp(-t / tau), "-", label="Analytical")
ax.plot(sol.t, sol.y[0], "o", label="RK45")
ax.legend()
ax.grid()

plt.show()

10.5. Διαφορικές εξισώσεις ανώτερης τάξης

Οι αριθμητικές μέθοδοι που περιγράφηκαν παραπάνω είναι σχεδιασμένες για την επίλυση διαφορικών εξισώσεων πρώτης τάξης. Υπάρχουν όμως περιπτώσεις που καλούμαστε να λύσουμε διαφορικές εξισώσεις ανώτερης τάξης. Μια τέτοια περίπτωση είναι η επίλυση του δευτέρου νόμου του Νεύτωνα, όταν γνωρίζουμε τις αρχικές συνθήκες θέσης και ταχύτητας.

Exercise 10.5

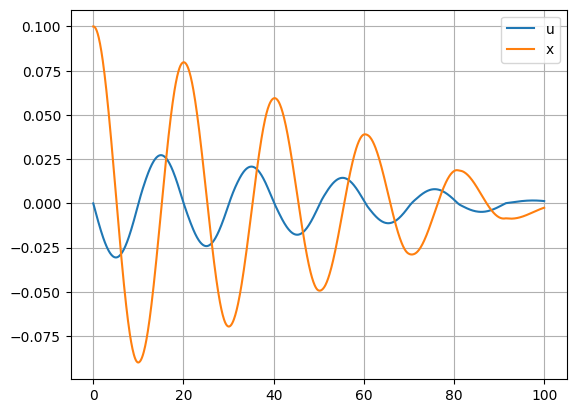
Έστω ένα σώμα μετακινείται σε οριζόντιο επίπεδο ενώ είναι συνδεδεμένο με ελατήριο σταθεράς \(k=0.1 \text{N/m}\). Το σώμα έρχεται σε επαφή δέχεται από το επίπεδο δύναμη τριβής αντίθετη με την ταχύτητά του. Δίνεται η μάζα του σώματος \(m=1\text{kg}\), η επιτάχυνση της βαρύτητας \(g=10\text{m/s}^2\) και ο συντελεστής τριβής \(\mu=5\times 10^{-5}\). Στον χρόνο μηδέν το σώμα είναι ακίνητο \(0.1m\) μακρυά από το σημείο ισορροπίας. Υπολογίστε την θέση και την ταχύτητα του σώματος για το χρονικό διάστημα 0 έως \(100\text{s}\) με βήμα \(0.1\text{s}\) και απεικονίστε τα αποτελέσματα σε γραφική παράσταση.

Solution to Exercise 10.5

Το ισοζύγιο δυνάμεων στο σώμα εκφράζεται ως:

\[ \DeclareMathOperator{\sgn}{sgn} m \frac{d^2 x}{dt^2}=-kx-\mu mg\sgn (u) \]

όπου sgn, η συνάρτηση πρόσημου.

H διαφορική εξίσωση ορίζεται με δεύτερη παράγωγο, μπορούμε όμως να μειώσουμε την τάξη του προβλήματος, συμπεριλαμβάνοντας την ταχύτητα στις εξαρτημένες μεταβλητές μας:

\[\begin{split} y= \begin{bmatrix} x\\ u \end{bmatrix} \end{split}\]

οπότε η εξίσωσή μας μετατρέπεται στο σύστημα:

\[\begin{split} \DeclareMathOperator{\sgn}{sgn} \begin{aligned} \frac{d x}{dt}&=&u \\ \frac{d u}{dt}&=&-\frac{k}{m}x-\mu g\sgn (u) \end{aligned} \end{split}\]

Το σύστημα μας ορίζεται με παραγώγους πρώτης τάξης και μπορεί να λυθεί με τις μεθόδους για προβλήματα αρχικής τιμής. Η αρχική κατάσταση δίνεται ως:

\[\begin{split} y(0)= \begin{bmatrix} x_0\\ u_0 \end{bmatrix} = \begin{bmatrix} 0.1\\ 0 \end{bmatrix} \end{split}\]

και το διάνυσμα των πρώτων παραγώγων:

\[\begin{split} \frac{dy}{dt}= \begin{bmatrix} y_1(t)\\ -\frac{k}{m}y_0(t)-\mu g\sgn (y_1(t)) \end{bmatrix} \end{split}\]

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

dt = 0.1  # s
mu = 5e-5
k = 0.1  # N/m
m = 1  # kg
g = 10  # m/s2

t = np.arange(0.0, 100.0 + dt / 2, dt)


def dydt(t: float, y: np.ndarray) -> np.ndarray:
    return np.array([y[1], -k / m * y[0]] - mu * g * np.sign(y[1]))


sol = solve_ivp(dydt, [0, 100], [0.1, -0.0], t_eval=t)

fig, ax = plt.subplots()
ax.plot(sol.t, sol.y[1], label="u")
ax.plot(sol.t, sol.y[0], label="x")
ax.legend()
ax.grid()

plt.show()

H λογική του προηγούμενου παραδείγματος έχει εφαρμογή σε προβλήματα αρχικής τιμής που εκφράζονται από διαφορική εξίσωση οποιασδήποτε τάξης \(n\). Με δεδομένη την διαφορική εξίσωση:

\[ f^{(n)}=F(t,f(t),f'(t),\dots,f^{(n-1)}(t)) \]

αρκεί να ορίσουμε τις εξαρτημένες \(n\) μεταβλητές μας ως:

\[\begin{split} y= \begin{bmatrix} f(t)\\ f'(t)\\ \dots\\ f^{(n-1)} \end{bmatrix} \end{split}\]

και το διάνυσμα των πρώτων παραγώγων ως:

\[\begin{split} \frac{dy}{dt}= \begin{bmatrix} f'(t)\\ f''(t)\\ \dots\\ f^{(n)} \end{bmatrix} = \begin{bmatrix} y_1(t)\\ y_2(t)\\ \dots\\ F(t,y_0(t),y_1(t),\dots,y_{n-1}(t)) \end{bmatrix} \end{split}\]