3. Αριθμητική κινητής υποδιαστολής#
3.1. Χρήση πραγματικών αριθμών#
Η αριθμητική ανάλυση εφαρμόζεται στην επίλυση προβλημάτων με πραγματικούς αριθμούς. Διαισθητικά δίνουμε έμφαση μόνο στα πρώτα ψηφία ενός πραγματικού αριθμού. Παρακάτω αυτό θα το ονομάσουμε σημαντικό μέρος. Επιπλέον χρησιμοποιούμε ακέραιες δυνάμεις του δέκα όταν μετράμε πολύ μικρά ή πολύ μεγάλα μεγέθη. Τις δυνάμεις αυτές της κρύβουμε συχνά μέσα στις μονάδες.
Μπορούμε επομένως με το σημαντικό μέρος κι έναν ακέραιο εκθέτη του δέκα να καταγράψουμε πραγματικούς αριθμούς οποιουδήποτε μεγέθους, έχοντας πάντα κατά νου ότι τα τελευταία δεκαδικά έχουν μικρότερη σημασία και συχνά παραλείπονται ή στρογγυλοποιούνται.
3.2. Επιστημονική σημειογραφία#
Θα ονομάσουμε επιστημονική σημειογραφία ή επιστημονική μορφή την αποτύπωση πραγματικών αριθμών με την μορφή:
Στα ψηφιακά συστήματα χρησιμοποιούνται αριθμοί κινητής υποδιαστολής ή αλλιώς αριθμοί μηχανής (float) για την διαχείριση πραγματικών αριθμών. Για την ευκολότερη απεικόνιση τους χρησιμοποιείται μια ψηφιακή εκδοχή της επιστημονικής σημειογραφίας με το γράμμα e:
όπου
\(m\) σημαντικό μέρος (mantissa ή significand): δεκαδικός αριθμός, συνήθως στο διάστημα 1 έως 10
\(n\) εκθέτης (exponent ή radix): ακέραια τιμή
\(b\) βάση: 10
Δεκαδική μορφή |
Επιστημονική μορφή |
Επιστημονική μορφή (ψηφιακή) |
|---|---|---|
5 |
\(5\cdot 10^0\) |
5e0 |
-200 |
\(-2 \cdot 10^2\) |
-2e2 |
1234.567 |
\(1.234567 \cdot 10^3\) |
1.234567e3 |
3450000000 |
\(3.45 \cdot 10^9\) |
3.45e9 |
0.2 |
\(2 \cdot 10^{−1}\) |
2e-1 |
0.00000000345 |
\(3.45 \cdot 10^{−9}\) |
3.45e-9 |
Εναλλακτικά μπορεί να χρησιμοποιηθεί το κεφαλαίο E, ενώ σε ορισμένα προγραμματιστικά περιβάλλοντα (Fortran, Matlab) υποστηρίζεται επιπλέον το d και D.
Radius_Earth = 6378e3 # m
Diameter_hair = 70e-6 # m
print(f"{Radius_Earth:g} {Diameter_hair:g}")
6.378e+06 7e-05
3.3. Εσωτερική αναπαράσταση#
Τα ψηφιακά συστήματα χρησιμοποιούν την ψηφιακή εκδοχή της επιστημονικής σημειογραφίας κατά την αποτύπωση των αριθμών μηχανής (δεκαδικό σύστημα). Εσωτερικά όμως χρησιμοποιούν το δυαδικό σύστημα. Το πλήθος της μνήμης που καταλαμβάνει ένας αριθμός κινητής υποδιαστολής καθορίζεται από την αρχιτεκτονική του επεξεργαστή. Συνήθως χρησιμοποιείται ο αριθμός κινητής υποδιαστολής διπλής ακρίβειας, ο οποίος καταλαμβάνει 64 bit με την εξής κατανομή:
1 bit στο πρόσημο (sign),
11 bit στον εκθέτη (exponent),
52 bit (\(b_0\dots b_{51}\)) στο κλασματικό μέρος (fraction ή mantissa).

Fig. 3.1 Αναπαράσταση στην μνήμη ενός αριθμού μηχανής διπλής ακρίβειας σύμφωνα με το πρότυπο IEEE 754. (Πηγή: Wikipedia Commons)#
Η εσωτερική αναπαράσταση έχει την μορφή:
Στην επιστημονική σημειογραφία το σημαντικό μέρος παίρνει συνήθως τιμές στο πεδίο \([1,10)\), ενώ στην εσωτερική αναπαράσταση κυμαίνεται στο πεδίο \([1,2)\). Αυτό συμβαίνει πάντα στις κανονικοποιημένες τιμές στις οποίες το πρώτο ψηφίο είναι υποχρεωτικά 1. Γι’αυτό, από τον τον αριθμό \(1.F\) δηλώνεται ρητά μόνο το κλασματικό μέρος (\(F\)) εξοικονομώντας ένα bit (άρρητη μονάδα). Εξαίρεση αποτελούν οι ειδικές τιμές, οι οποίες όμως διαχωρίζονται με τις ακραίες τιμές του εκθέτη \(e\). Σημειώνεται ότι η δύναμη περιλαμβάνει έναν όρο μετατόπισης (offset) 1023, έτσι ώστε το \(e\) να είναι θετικός αριθμός. Περισσότερες λεπτομέρειες δίνονται στο πρότυπο IEEE 754 και στις αναθεωρήσεις του.
Exercise 3.1
Μία μονάδα γραφικού επεξεργαστή (GPU) για εκπαίδευση μοντέλων τεχνητής νοημοσύνης έχει αρχιτεκτονική FP8 (E4M3). Πόσα bit χρησιμοποιεί η GPU για έναν αριθμό μηχανής και πώς τα κατανέμει;
Solution to Exercise 3.1
8 bit συνολικά (FP_)
4 bit για τον εκθέτη (E_)
3 bit για το κλασματικό μέρος (M_)
1 bit για το πρόσημο (εννοείται)
3.4. Ειδικές τιμές#
Οι ακραίες τιμές του εκθέτη χρησιμοποιούνται για τον ορισμό ειδικών τιμών.
Ειδική τιμή |
Συντομογραφία |
Πρόσημο \((sign)\) |
Εκθέτης \((e)\) |
Κλασματικό μέρος \((F)\) |
|---|---|---|---|---|
Signed zero |
\(\pm 0\) |
0 ή 1 |
\(00000000000_2\) |
\(0\) |
Subnormal numbers |
\(\pm 0.F\) |
0 ή 1 |
\(00000000000_2\) |
\(\neq 0\) |
Infinite |
\(\pm \text{Inf}\) |
0 ή 1 |
\(11111111111_2\) |
\(0\) |
Not a Number |
\(\text{NaN}\) |
0 ή 1 |
\(11111111111_2\) |
\(\neq 0\) |
Οι μη κανονικοποιημένες τιμές (subnormal) χρησιμοποιούνται για την αναπαράσταση πολύ μικρών αριθμών με μειωμένο όμως αριθμό σημαντικών ψηφίων. Έχουν μηδέν στην θέση της άρρητης μονάδας, επομένως η εσωτερική αναπαράσταση είναι της μορφής \(0.F\). Αν αυτές οι τιμές κανονικοποιηθούν, δίνουν τιμή μηδέν. Ο χειρισμός των μη κανονικοποιημένων τιμών ελέγχεται από τις παραμέτρους του μεταγλωττιστή (compiler).
Οι πράξεις με ειδικές τιμές δίνουν το αναμενόμενο μαθηματικό αποτέλεσμα, εκτός από τις παρακάτω περιπτώσεις:
Οι πράξεις \(\frac{0}0, \frac{\infty}{\infty},\infty - \infty,0 \times \infty\) έχουν απροσδιόριστο αποτέλεσμα (\(\text{NaN}\)).
Οι δυνάμεις \( 0^0, 1^{\infty}, \infty^0\) μαθηματικά δίνουν απροσδιόριστο, αλλά στους υπολογιστές δίνουν 1.
Οποιαδήποτε πράξη με \(\text{NaN}\) έχει ως αποτέλεσμα \(\text{NaN}\).
Tip
Στις διαιρέσεις πρέπει διαχειρίζεστε κατάλληλα την περίπτωση μηδενικού παρονομαστή.
Το μηδέν μπορεί να πάρει αρνητικό πρόσημο (signed zero).
import numpy as np
print(np.float64(-0.0))
-0.0
Τα παρακάτω παραδείγματα οδηγούν σε υπερχείλιση και υποχείλιση χωρίς καμία αναφορά λάθους.
print(np.float64(1e400)) # Overflow
print(np.float64(1e-400)) # Underflow
inf
0.0
Αντίθετα οι υπολογισμοί που οδηγούν σε άπειρο ή απροσδιόριστο αποτέλεσμα προκαλούν την αναφορά προειδοποίησης.
print(1 / np.float64(-0.0))
print(np.float64(0.0) / np.double(0.0))
print(np.inf * np.float64(0.0))
-inf
nan
nan
/tmp/ipykernel_318458/267969433.py:1: RuntimeWarning: divide by zero encountered in scalar divide
print(1 / np.float64(-0.0))
/tmp/ipykernel_318458/267969433.py:2: RuntimeWarning: invalid value encountered in scalar divide
print(np.float64(0.0) / np.double(0.0))
/tmp/ipykernel_318458/267969433.py:3: RuntimeWarning: invalid value encountered in scalar multiply
print(np.inf * np.float64(0.0))
Για να ελέγξετε αν μία μεταβλητή έχει πάρει απροσδιόριστη τιμή, χρησιμοποιείστε την numpy.isnan[1].
print(np.isnan(np.nan + 1.0))
True
3.5. Απόσταση αριθμών μηχανής#
Δύο διαδοχικοί ακέραιοι αριθμοί έχουν πάντα σταθερή απόσταση μεταξύ τους μία μονάδα. H σταθερή απόσταση δεν υφίσταται στους οι αριθμούς μηχανής καθώς εκτός από το τελευταίο σημαντικό ψηφίο, μπορεί να αλλάξει κι ο εκθέτης. Όπως φαίνεται στο παρακάτω γράφημα, οι αριθμοί μηχανής είναι πιο πυκνοί σε μικρές απόλυτες τιμές και αραιώνουν σε μεγαλύτερες.
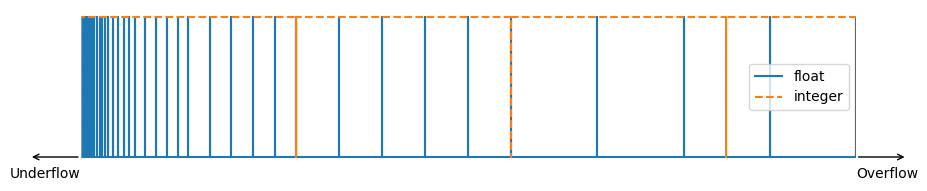
Fig. 3.2 Αποστάσεις μεταξύ ακεραίων αριθμών και αριθμών κινητής υποδιαστολής.#
Η συνάρτηση numpy.spacing δίνει την απόλυτη απόσταση ανάμεσα σε έναν αριθμό κινητής υποδιαστολής και τον γειτονικό του.
import numpy as np
print(np.spacing(1.0))
print(np.spacing(10.0))
2.220446049250313e-16
1.7763568394002505e-15
3.6. Όρια αριθμών μηχανής#
Η συνάρτηση sys.float_info παρουσιάζει πληροφορίες για την εσωτερική αναπαράσταση του τύπου float που χρησιμοποιείται από το ψηφιακό σύστημα.
import sys
print(sys.float_info)
sys.float_info(max=1.7976931348623157e+308, max_exp=1024, max_10_exp=308, min=2.2250738585072014e-308, min_exp=-1021, min_10_exp=-307, dig=15, mant_dig=53, epsilon=2.220446049250313e-16, radix=2, rounds=1)
Παράμετρος |
Περιγραφή |
Τιμή |
|---|---|---|
min_exp |
ελάχιστη δύναμη |
-1021 |
max_exp |
μέγιστη δύναμη |
1024 |
mant_dig (\(t\)) |
σημαντικά ψηφία |
53 |
radix (\(b\)) |
βάση |
2 |
rounds |
σύστημα στρογγυλοποίησης[2] |
1 |
Επιπλέον παρουσιάζονται τα αντίστοιχα όρια για την αναπαράσταση του τύπου float σε επιστημονική μορφή.
Παράμετρος |
Περιγραφή |
Τιμή |
|---|---|---|
max |
μέγιστη τιμή |
1.7976931348623157e+308 |
max_10_exp |
μέγιστη δύναμη[3] |
308 |
min |
ελάχιστη κανονικοποιημένη τιμή |
2.2250738585072014e-308 |
min_10_exp |
ελάχιστη δύναμη |
-307 |
dig (\(t\)) |
σημαντικά ψηφία |
15 |
epsilon (\(ε_M)\) |
έψιλον της μηχανής |
2.220446049250313e-16 |
import numpy as np
print(np.finfo(np.float64))
print(np.finfo(np.float64).eps, np.finfo(np.float64).tiny)
Machine parameters for float64
---------------------------------------------------------------
precision = 15 resolution = 1.0000000000000001e-15
machep = -52 eps = 2.2204460492503131e-16
negep = -53 epsneg = 1.1102230246251565e-16
minexp = -1022 tiny = 2.2250738585072014e-308
maxexp = 1024 max = 1.7976931348623157e+308
nexp = 11 min = -max
smallest_normal = 2.2250738585072014e-308 smallest_subnormal = 4.9406564584124654e-324
---------------------------------------------------------------
2.220446049250313e-16 2.2250738585072014e-308
Tip
Οι τιμές στο διάστημα [4.9406564584124654e-324,2.2250738585072014e-308) είναι μη κανονικοποιημένες, δηλαδή ξεκινάνε με μηδενικά και όχι την άρρητη μονάδα. Γι’ αυτό το λόγο έχουν λιγότερα σημαντικά ψηφία και μικρότερη ακρίβεια.
Ορισμός
Το έψιλον ή μηδέν της μηχανής (\(ε_M\)) εκφράζει την σχετική απόσταση ανάμεσα σε δύο διαδοχικούς αριθμούς μηχανής. Ένας εναλλακτικός ορισμός του \(ε_M\) είναι απόσταση του 1 από τον γειτονικό του αριθμό.
3.7. Ποσοτικοποίηση των σφαλμάτων#
Για την ποσοτικοποίηση των σφαλμάτων χρησιμοποιούνται δύο προσεγγίσεις:
Το απόλυτο σφάλμα
Το σχετικό σφάλμα
όπου:
\(x\) η εκτίμηση μίας μεταβλητής και
\(x_r\) η πραγματική τιμή της η απλώς μια καλύτερη εκτίμηση.
Κατά τον έλεγχο των σφαλμάτων ορίζεται συνήθως ένα ανώτατο όριο πέρα από το οποίο το αποτέλεσμα του υπολογισμού μας δεν είναι αποδεκτό. Το όριο αυτό ονομάζεται ανοχή \(TOL\) (tolerance) και εφαρμόζεται συνήθως στην σχετική τιμή του σφάλματος.
Η επιλογή του σφάλματος και της ανοχής μπορεί να διαφέρουν κατά περίπτωση. Για παράδειγμα, όταν οι τιμές μας προσεγγίζουν το μηδέν, ενδείκνυται η χρήση του απόλυτου σφάλματος.
Exercise 3.2
Υπολογίστε το απόλυτο και σχετικό σφάλμα της τιμής 3.14 σε σχέση με τον αριθμό π της βιβλιοθήκης NumPy. Ελέγξτε αν το σχετικό σφάλμα ικανοποιεί μια ανοχή 0.1%.
Solution to Exercise 3.2
import numpy as np
E = 3.14 - np.pi
e = (3.14 - np.pi) / np.pi
TOL = 0.1 / 100
print(E)
print(e)
print(f"{e:.2%}")
print(np.abs(e) < TOL)
-0.0015926535897929917
-0.0005069573828972128
-0.05%
True
3.8. Σφάλματα τεμαχισμού και στρογγυλοποίησης#
Εκτός ιδανικών καταστάσεων, ένας πραγματικός αριθμός βρίσκεται στο ενδιάμεσο διάστημα μεταξύ δύο διαδοχικών αριθμών μηχανής. Κατά την αποθήκευση του πραγματικού αριθμού ως αριθμού μηχανής ο υπολογιστής καλείται να επιλέξει μία από τις δύο τιμές εφαρμόζοντας:
Τεμαχισμό, δηλαδή να απορρίψει όσα ψηφία του πραγματικού δεν χωράνε στην εσωτερική αναπαράσταση με σχετικό σφάλμα:
\[ |ε|\leq b^{1-t} \]Στρογγυλοποίηση, δηλαδή να στρογγυλοποιήσει τον πραγματικό αριθμό στον κοντινότερο αριθμό μηχανής με σχετικό σφάλμα:
\[ |ε|\leq\frac{1}{2}b^{1-t} \]Το μέγεθος \(u=\frac{1}{2}b^{1-t}\) καλείται και μοναδιαίο σφάλμα στρογγυλοποίησης.
Στην ακραία περίπτωση της ισότητας το σφάλμα της στρογγυλοποίησης είναι το μισό του σφάλματος τεμαχισμού και γι’ αυτό εφαρμόζεται σχεδόν πάντα στους υπολογιστές. Στο υπόλοιπο μέρος του συγγράμματος θα αναφερθούμε αποκλειστικά στο σφάλμα στρογγυλοποίησης (round-off error). Σημειώνεται ότι στρογγυλοποίηση εφαρμόζεται και μετά από οποιαδήποτε μαθηματική πράξη στον υπολογιστή.
print(10 - 9.99 == 0.01)
print(10 - 9.99)
False
0.009999999999999787
Το σφάλμα στρογγυλοποίησης μεγεθύνεται μετά από διαδοχικούς υπολογισμούς.
x = 1
dx = 1 / 3
n = 100000
for i in range(n):
x = x - dx
for i in range(n):
x = x + dx
print(x)
0.9999999999980784
Λόγω του σφάλματος στρογγυλοποίησης συνήθως δεν έχει νόημα να ελέγχουμε την ισότητα δύο αριθμών μηχανής, αλλά το σφάλμα, σχετικό ή/και απόλυτο. Για αυτή την περίπτωση η NumPy παρέχει την συνάρτηση isclose με προεπιλεγμένα όρια rtol=1e-05, atol=1e-08.
print(10 - 9.99 == 0.01)
print(np.isclose(10 - 9.99, 0.01, rtol=1e-07))
False
True
Αντίστοιχα για τον έλεγχο ισότητας δύο πινάκων (στοιχείο προς στοιχείο) χρησιμοποιείται η συνάρτηση allclose.
Exercise 3.3
Για έναν αριθμό κινητής υποδιαστολής με 53 σημαντικά ψηφία στο δυαδικό σύστημα, υπολογίστε το μέγιστο σχετικό σφάλμα τεμαχισμού και στρογγυλοποίησης:
Solution to Exercise 3.3
Εδώ \(ε_{chop}=ε_Μ\).
3.9. Πηγές σφαλμάτων#
Τόσο στους αναλυτικούς υπολογισμούς, όσο και στους υπολογισμούς με αριθμούς μηχανής υπεισέρχονται σφάλματα. Αν και γενικώς προσπαθούμε να τα περιορίσουμε, αυτό δεν είναι απόλυτα εφικτό. Οι πηγές σφαλμάτων στους αριθμητικούς υπολογισμούς είναι:
Η υπερχείλιση (overflow).
Αποτελέσματα μεγαλύτερα από το άνω όριο παίρνουν την ειδική τιμή Inf.
Η υποχείλιση (underflow).
Αποτελέσματα μικρότερα από το κάτω όριο παίρνουν την τιμή 0.
Η στρογγυλοποίηση
Όλα τα αποτελέσματα πράξεων στρογγυλοποιούνται στους αντίστοιχους αριθμούς κινητής υποδιαστολής.
Η αποκοπή
Σφάλματα που εισάγει η αριθμητική μέθοδος λόγω της χρήσης πεπερασμένων όρων ή αντί άπειρων.
Important
Σε πολλά συγγράμματα ο όρος σφάλμα αποκοπής (truncation error) χρησιμοποιείται ως συνώνυμο του σφάλματος τεμαχισμού (chopping error). Το παρόν σύγγραμμα υιοθετεί την ορολογία των Chapra και Canale [2], που διαχωρίζει τις δύο έννοιες.
Στα πλαίσια της αριθμητικής ανάλυσης είναι απαραίτητη η ποσοτικοποίηση των σφαλμάτων και η κατανόηση των παραγόντων που τα επηρεάζουν. Οι πρώτες 3 πηγές σφαλμάτων μπορούν να περιοριστούν χρησιμοποιώντας αριθμούς κινητής υποδιαστολής υψηλότερης ακρίβειας, π.χ. διπλής ή αντί για μονής, καθώς επίσης και με την αναδιατύπωση ορισμένων αναλυτικών σχέσεων. Η τελευταία πηγή σφαλμάτων μπορεί να περιοριστεί με την κατάλληλη επιλογή της αριθμητικής μεθόδου και των παραμέτρων της, όπως θα δούμε στα παρακάτω κεφάλαια.
Exercise 3.4
Υπολογίστε τις ρίζες της συνάρτησης \(f(x)=x^2-100000.1x+10000\).
Solution to Exercise 3.4
import numpy as np
a = 1
b = -100000.1
c = 10000
x1 = (-b + np.sqrt(b**2 - 4 * a * c)) / (2 * a)
x2 = (-b - np.sqrt(b**2 - 4 * a * c)) / (2 * a)
print(x1, x2)
100000.0 0.10000000000582077
Ακόμη κι όταν υπάρχουν αναλυτικές λύσεις χρειάζεται προσοχή στην υλοποίηση σε κώδικα μίας μαθηματικής έκφρασης. Στην παραπάνω άσκηση οι ρίζες του τριωνύμου είναι οι γνωστές τιμές 100000 και 0.1. Όπως φαίνεται από τα αποτελέσματα, ο υπολογισμός της δεύτερης ρίζας αποκλίνει ελαφρώς και αυτό οφείλεται στο σφάλμα στρογγυλοποίησης κατά την αφαίρεση στον αριθμητή. Ένας τρόπος να περιοριστεί το σφάλμα είναι να χρησιμοποιηθεί η εναλλακτική σχέση:
Η πρώτη ρίζα υπολογίζεται με \(-\) και η δεύτερη με \(+\).
Exercise 3.5
Λύστε την Άσκηση 3.4 με την εναλλακτική σχέση.
Solution to Exercise 3.5
import numpy as np
a = 1
b = -100000.1
c = 10000
x1 = (2 * c) / (-b - np.sqrt(b**2 - 4 * a * c))
x2 = (2 * c) / (-b + np.sqrt(b**2 - 4 * a * c))
print(x1, x2)
99999.99999417923 0.1
3.10. Ταχύτητα υπολογισμού#
Exercise 3.6
Χρησιμοποιώντας την μονάδα κώδικα timeit, μετρήστε τον χρόνο που χρειάζονται οι 4 βασικοί αριθμητικοί τελεστές, η δύναμη και η συνάρτηση exp της NumPy και αδιαστατοποιήστε τα αποτελέσματα σε σχέση με τον χρόνο της πρόσθεσης. Προσέξτε ότι τα αποτελέσματα διαφοροποιούνται ελαφρώς αναλόγως τις αριθμητικές τιμές που θα επιλεγούν για τις πράξεις.
Solution to Exercise 3.6
import timeit
import numpy as np
a = np.arange(0, 20, 0.1)
b = 2.5
iterations = 100000
def time_operation(operation: str) -> float:
return timeit.timeit(stmt=operation, number=iterations, globals=globals())
dt_addition = time_operation("c=a+b")
# first call is always longer. Second call is more accurate
dt_addition = time_operation("c=a+b")
print(f"{'Πρόσθεση':15} {1.0}")
print(f"{'Αφαίρεση':15} {time_operation('c=a-b') / dt_addition}")
print(f"{'Πολλαπλασιασμός':15} {time_operation('c=a*b') / dt_addition}")
print(f"{'Διαίρεση':15} {time_operation('c=a/b') / dt_addition}")
print(f"{'Δύναμη':15} {time_operation('c=a**b') / dt_addition}")
print(f"{'Εκθετική συν.':15} {time_operation('c=np.exp(a)') / dt_addition}")
Πρόσθεση 1.0
Αφαίρεση 0.9720733059079744
Πολλαπλασιασμός 0.9643400915518345
Διαίρεση 1.0550197357425979
Δύναμη 5.104914387553147
Εκθετική συν. 1.956725912316177
Ως μέτρο υπολογιστικής επίδοσης χρησιμοποιούνται τα flop/s ή FLOPS, δηλαδή το πλήθος των πράξεων κινητής υποδιαστολής που εκτελεί ένας υπολογιστής στην μονάδα του χρόνου (συνήθως σε ένα δευτερόλεπτο). Τα FLOPS μπορεί να διαφοροποιηθούν σημαντικά ανάλογα με το τρόπο μέτρησης για αυτό θέλει προσοχή όταν αναφέρονται τέτοιες τιμές. Οι υπολογιστές υψηλών επιδόσεων έχουν ξεπεράσει τα \(1\text{Eflop/s}=1\times 10^{18} \text{flop/s}\) σύμφωνα με την λίστα που διατηρεί ο δικτυακός τόπος TOP500.
Exercise 3.7
Ένας απλός τρόπος εκτίμησης των FLOPS συνίσταται στην μέτρηση του χρόνου που χρειάζεται ένας υπολογιστής για να εκτελέσει έναν πολλαπλασιασμό και μία πρόσθεση μαζί (multiply-and-add instruction), δηλαδή \(y←a+x*y\), μαζί με τον χρόνο που απαιτείται για την ανάκτηση από την μνήμη των δεδομένων που εμπλέκονται στις δύο αυτές πράξεις. Εκτιμήστε τα FLOPS του υπολογιστή σας με βάση τον παραπάνω ορισμό.
Solution to Exercise 3.7
import timeit
import numpy as np
def FLOP_function(iterations: int):
x = 1 + 1e-10
y = 1.0
a = 0.5
for i in range(iterations):
y = a + x * y
# print(y) #Make sure y does not reach infinity
iterations = 10000000
dt = timeit.timeit(stmt="FLOP_function(iterations)", number=1, globals=globals())
FLOPS = 2 * iterations / dt # MAD instruction counts as 2 iterations
print(f"{FLOPS * 1e-6:.2f} Mflop/s")
63.16 Mflop/s
