7. Ολοκλήρωση

7.1. Διατύπωση του προβλήματος

\[I= \int_{a}^{b}f\left(x\right) dx = F(b)-F(a)\]

όπου \(\frac{dF(x)}{dx}=f(x)\).

Exercise 7.1

Να υπολογιστεί το ολοκλήρωμα της συνάρτησης \( f(x)=x^2 \) από 0 έως 10.

\[F(x)=\frac{1}{3}x^3\]

\[I= \int_{0}^{10} x^2 dx = F(10)-F(0)=\frac{1}{3}10^3-0=\frac{1000}{3}\approx 333.33\]

Note

Δεν μπορούν να ολοκληρωθούν όλες οι συναρτήσεις αναλυτικά. π.χ. \({e^{-x^2}}\).

7.2. Γραφική ολοκλήρωση

Πολλές φορές η συνάρτησή δίνεται ως μία σειρά \(n\) σημείων.

Exercise 7.2

Να παρασταθεί γραφικά η συνάρτηση \( f(x)=x^2 \) από 0 έως 10 και να εκτιμηθεί γραφικά το ολοκλήρωμά της στο ίδιο διάστημα.

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(0, 10 + 1, 1)
y = x**2

fig, ax = plt.subplots()
ax.set(xlabel="x", ylabel="y")
ax.plot(x, y, "^-r")
ax.fill_between(x, 0, y)
ax.grid()

plt.show()

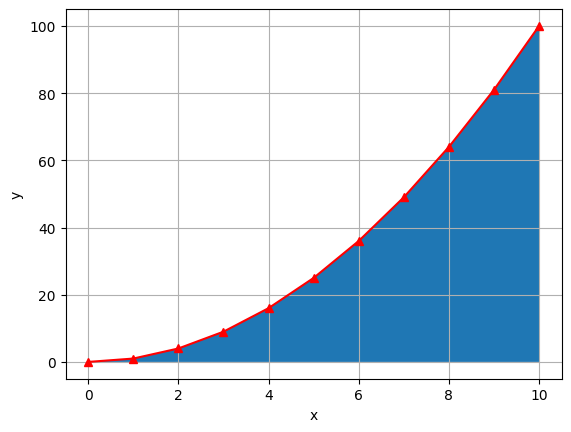
Το εμβαδόν κάτω από την καμπύλη αντιπροσωπεύει το ολοκλήρωμα. Κάθε ορθογώνιο στο γράφημα αντιπροσωπεύει \(2*20=40\) μονάδες επιφάνειας. 6 (σχεδόν) ολόκληρα ορθογώνια + 5 μισά = 8.5, άρα:

\[8.5*40=340\]

7.3. Μέθοδος Riemann

Αν έχουμε \(n+1\) σημεία (\(x_0,\dots,x_n\)), προκύπτουν \(n\) διαστήματα.

\[h_i=x_{i+1}-x_{i}\]

Για τα διαστήματα (\(h_0,\dots,h_{n-1}\)) ξεκινάμε την αρίθμηση από το 0 όπως και στα σημεία για λόγους συμβατότητας με την αρίθμηση της Python. Αν θεωρήσουμε ότι αυτά τα διαστήματα έχουν το ίδιο πλάτος, τότε \(h=\frac{b-a}{n}\).

\[\begin{split} \begin{align} x_0=a=0\\ x_1=x_0+h=1\\ \dots\\ x_i=x_{i-1}+h\\ \end{align} \end{split}\]

Για κάθε διάστημα υπολογίζουμε την επιφάνεια με τον τύπο του ορθογωνίου, επομένως:

\[I= \int_{a}^{b}f\left(x\right) dx \approx \sum_{i=0}^{n-1} h f(x_{i+1}) = h \sum_{i=0}^{n-1} f(x_{i+1})\]

χρησιμοποιώντας για ύψος το δεξιό άκρο κάθε διαστήματος \(f(x_{i+1})\).

Στο προηγούμενο παράδειγμα προκύπτει \(h=1\) για \(n=10\).

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(0, 10 + 1, 1)
y = x**2
yint = y[1:]    #Integrating with right y

fig, ax = plt.subplots()
ax.set(xlabel="x", ylabel="y")
ax.fill_between(x, 0, y)
ax.bar(x[:-1], height=yint, fill=False, width=1.0, align="edge", edgecolor="r")
# ax.grid()

plt.show()

integral_num = 1 * np.sum(yint)
integral_an = 1000 / 3
print("integral_num=", integral_num)
print(f"Rel_error={(integral_num-integral_an)/integral_an:.1%}")

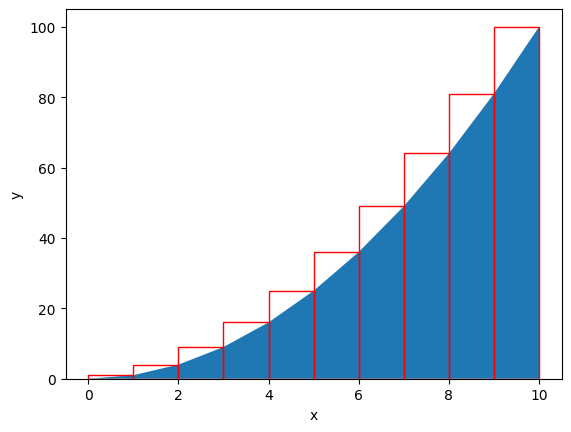
integral_num= 385
Rel_error=15.5%

Tip

H συνάρτηση numpy.sum είναι βελτιστοποιημένη και παρέχει επιπλέον δυνατότητες για πίνακες της NumPy από την γενικής χρήσης sum της Python.

Η μέθοδος αυτή ονομάζεται κανόνας του Riemann και μπορεί να εφαρμοστεί για το αριστερό άκρο \(x_{i}\), δεξί άκρο \(x_{i+1}\) ή το μέσο \(\frac{x_{i}+x_{i+1}}{2}\).

Στο παράδειγμά μας η μέθοδος αυτή υπερεκτιμά το αποτέλεσμα. Πώς θα αλλάξει το σφάλμα

• αν χρησιμοποιήσουμε το αριστερό άκρο ή την τιμή στο μέσο;

• αν η \(f(x)\) είναι γνησίως φθίνουσα;

• αν η \(f(x)\) είναι ημιτονοειδής;

• αν μειώσουμε το διάστημα \(h\);

Αρχικά το ολοκλήρωμα \(I\) χωρίζεται σε επιμέρους διαστήματα:

\[I= \int_{a}^{b}f\left(x\right) dx = \sum^{n-1}_{i=0} \int_{x_{i}}^{x_{i+1}}f\left(x\right) dx \]

Για τον υπολογισμό των τμηματικών ολοκληρωμάτων εφαρμόζεται η σειρά Taylor στην συνάρτηση \(f(x)\):

\[f(x)=f(x_i)+\frac{f'(x_i)}{1!}(x-x_i)^1+\frac{f''(x_i)}{2!}(x-x_i)^2+\dots\]

Κάθε διάστημα υπολογίζεται προσεγγιστικά με αποκοπή του όρων της πρώτης παραγώγου και ανώτερων. Ο όρος της πρώτης παραγώγου μας δίνει την τάξη μεγέθους του σφάλματος:

\[\int_{x_{i}}^{x_{i+1}}f\left(x\right) dx = \int_{x_{i}}^{x_{i+1}}(f(x_i)+f^\prime(x_i)(x-x_i)+\dots) dx \approx h f(x_i)+ \mathcal{O}(h^2)\]

Αν η ίδια διαδικασία εφαρμοστεί για το δεξί άκρο, η τάξη του σφάλματος είναι η ίδια:

\[\int_{x_{i}}^{x_{i+1}}f\left(x\right) dx \approx h f(x_{i+1})+ \mathcal{O}(h^2) \]

Το τελικό ολοκλήρωμα καθώς και το συνολικό σφάλμα του υπολογίζονται αθροίζοντας τα τμηματικά ολοκληρώματα και σφάλματα (\(n=\frac{b-a}h\)), επομένως:

\[\begin{split} \begin{align} I= \int_{a}^{b}f\left(x\right) dx \approx \sum_{i=0}^{n-1} [h f(x_{i+1})+ \mathcal{O}(h^2)] = h \sum_{i=0}^{n-1} f(x_{i+1})+ n \mathcal{O}(h^2) \\ = h \sum_{i=0}^{n-1} f(x_{i+1}) + \frac{b-a}{h} \mathcal{O}(h^2)=h \sum_{i=0}^{n-1} f(x_{i+1}) + \mathcal{O}(h) \end{align} \end{split}\]

7.4. Μέθοδος του τραπεζίου

Για καλύτερη ακρίβεια μπορούμε να αντικαταστήσουμε την σταθερή τιμή σε κάθε διάστημα με μια γραμμική συνάρτηση παρεμβολής. Έτσι προκύπτει ένα τραπέζιο σχήμα.

import matplotlib.pyplot as plt
import scipy.integrate as integrate
import numpy as np

x = np.arange(0, 10 + 1, 1)
y = x**2
yint = y[:-1]

fig, ax = plt.subplots()
ax.set(xlabel="x", ylabel="y")
ax.fill_between(x, 0, y)
ax.plot(x, y, "-r", x, y * 0, "-r")
ax.bar(x, height=y, fill=False, width=0.0, align="edge", edgecolor="r")
# ax.grid()

plt.show()

I_trapezoid = integrate.trapezoid(y, x)
I_analytical = 1000 / 3

print("integral_num=", I_trapezoid)
print(f"Rel_error={(I_trapezoid-I_analytical)/I_analytical:.1%}")

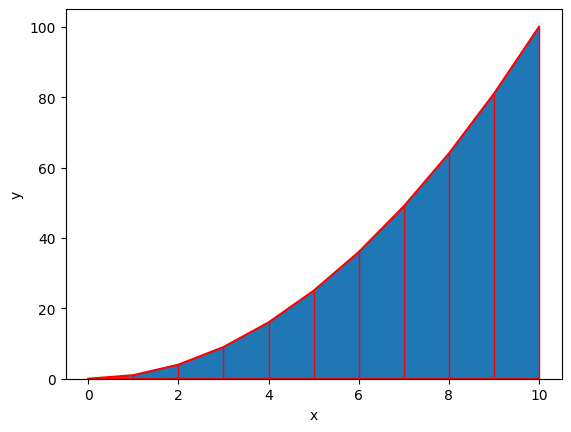
integral_num= 335.0
Rel_error=0.5%

Η μέθοδος του τραπεζίου ισοδυναμεί με τμηματική γραμμική παρεμβολή στα διαστήματα. Για την εκτίμηση του σφάλματος μπορεί να χρησιμοποιηθεί ένα πολυώνυμο ανώτερου βαθμού (δευτέρου), το οποίο μετά την ολοκλήρωση οδηγεί σε ένα σφάλμα τάξης \(h^3\):

\[\int_{x_i}^{x_{i+1}}f\left(x\right) dx \approx h \frac{f(x_i)+f(x_{i+1})}2 + \mathcal{O}(h^3)\]

Συνήθως το βήμα \(h\) είναι σταθερό, επομένως η παραπάνω σχέση οδηγεί στην συνολική έκφραση:

\[I= \int_{a}^{b}f\left(x\right) dx \approx \frac{h}{2}\left(f(x_0)+2\sum^{n-1}_{i=1} f(x_i)+ f(x_n)\right)+\mathcal{O}(h^2)\]

Η ακρίβεια της μεθόδου τραπεζίου είναι μια τάξη μεγέθους καλύτερη από την μέθοδο Riemann, δηλαδή \(\mathcal{O}(h^2)\) με αμελητέα αύξηση στο υπολογιστικό φορτίο. Η συνάρτηση numpy.trapz και η ισοδύναμη scipy.integrate.trapezoid παρέχουν έτοιμες υλοποιήσεις της μεθόδου του τραπεζίου, οι οποίες είναι κατάλληλες και για ανομοιόμορφα διαστήματα \(h_i\).

import numpy as np
from scipy.integrate import trapezoid

a = 0
b = np.pi
n = 11
h = (b - a) / (n - 1)
x = np.linspace(a, b, n)
f = np.sin(x)

I_sum = (h / 2) * (f[0] + 2 * np.sum(f[1 : n - 1]) + f[n - 1])
I_trapezoid = trapezoid(f, x)

print(I_sum)
print(I_trapezoid)

1.9835235375094546
1.9835235375094544

7.5. Κανόνες του Simpson

Η χρήση γραμμικών συναρτήσεων παρεμβολής στην μέθοδο του τραπεζίου εισάγει σφάλματα που θα μπορούσαν να περιοριστούν με την χρήση πολυωνύμων. Αυτή είναι η ιδέα πίσω από μια οικογένεια μεθόδων ολοκλήρωσης που ονομάζονται κανόνες του Simpson. Στον κανόνα 1/3 του Simpson, το πολυώνυμο είναι δευτέρου βαθμού, παίρνουμε 3 σημεία και υπολογίζουμε την ίδια συνάρτηση ανά δύο διαστήματα (\(2h\)):

\[\int_{x_i}^{x_{i+2}}f\left(x\right) dx \approx 2h \frac{f(x_i)+4f(x_{i+1})+f(x_{i+2})}6 + \mathcal{O}(h^5)\]

Το συνολικό άθροισμα στο διάστημα ολοκλήρωσης έχει τάξη σφάλματος \(\mathcal{O}(h^4)\).

Ιδανικά η μέθοδος εφαρμόζεται για άρτιο αριθμό διαστημάτων \(n\), αλλιώς πρέπει να γίνει ειδική διαχείριση στο πρώτο (\(h_0\)) ή στο τελευταίο διάστημα (\(h_n\)). Η συνάρτηση scipy.integrate.simpson αποτελεί υλοποίηση του κανόνα 1/3 του Simpson.

from scipy.integrate import simpson
import numpy as np

x = np.arange(0, 10 + 1, 1)
y = x**2

I_simpson = simpson(y, x)
I_analytical = 1000 / 3

print(f"Integral_simpson={I_simpson}")
print(f"Relative_error={(I_simpson-I_analytical)/I_analytical:.1%}")

Integral_simpson=333.3333333333333
Relative_error=0.0%

Στο κανόνα 3/8 του Simpson παρεμβάλουμε ένα πολυώνυμο τρίτου βαθμού σε διάστημα \(3h\) χρησιμοποιώντας 4 σημεία.

\[\int_{x_i}^{x_{i+3}}f\left(x\right) dx \approx 3h \frac{f(x_i)+3f(x_{i+1})+3f(x_{i+2}+f(x_{i+3})}8 + \mathcal{O}(h^5)\]

Ιδανικά η μέθοδος εφαρμόζεται για \(n\) πολλαπλάσιο του 3, αλλιώς πρέπει να γίνει ειδική διαχείριση στα πρώτα ή τα τελευταία διαστήματα. Επίσης μπορεί να χρησιμοποιηθεί σε συνδυασμό με τον κανόνα 1/3, αναλόγως το πλήθος των διαστημάτων.

Ο κανόνας 1/3 του Simpson συναντάται συχνότερα από τον κανόνα 3/8, καθώς έχει την ίδια τάξη ακρίβειας με λιγότερα σημεία.

7.6. Ειδικές περιπτώσεις

Οι συναρτήσεις ολοκλήρωσης της SciPy μπορούν να χρησιμοποιηθούν για διπλά ολοκληρώματα ή και περισσότερων διαστάσεων.

Επίσης ιδιαίτερα χρήσιμες είναι οι συναρτήσεις της SciPy που δέχονται απευθείας συναρτήσεις \(f(x)\), αντί για σειρές σημείων, όπως η scipy.integrate.quad. Σε αυτή την περίπτωση δηλώνεται η συνάρτηση που θα ολοκληρωθεί και τα όρια της ολοκλήρωσης και αποφασίζει η quad ποια μέθοδο θα χρησιμοποιήσει και πόσα σημεία χρησιμοποιώντας την βιβλιοθήκη QUADPACK[1]. H quad επιστρέφει μαζί με το αποτέλεσμα και μια εκτίμηση του απόλυτου σφάλματος.

from scipy.integrate import quad
import numpy as np

def f(x):
    return x**2

I_quad,err = quad(f,0,10)
I_analytical = 1000 / 3

print(f"Integral_numerical={I_quad}")
print(f"Estimated__absolute_error={err}")
print(f"Relative_error={(I_quad-I_analytical)/I_analytical:.1%}")

Integral_numerical=333.33333333333326
Estimated__absolute_error=3.700743415417188e-12
Relative_error=-0.0%

---

[1]

Piessens, Robert; de Doncker-Kapenga, Elise; Überhuber, Christoph W.; Kahaner, David (1983). QUADPACK: A subroutine package for automatic integration. Springer-Verlag. ISBN 978-3-540-12553-2.