5. Παρεμβολή και παλινδρόμηση

5.1. Διατύπωση του προβλήματος

Πολλές φορές αντί της μαθηματικής συνάρτησης \(y=f(x)\) μεταξύ δύο μεγεθών \(x\) και \(y\) είναι γνωστή μία σειρά από \(n\) σημεία \((x_i,y_i)\), η οποία περιγράφει προσεγγιστικά την εξάρτηση. Χαρακτηριστικό παράδειγμα είναι οι πίνακες που βρίσκονται στα παραρτήματα επιστημονικών βιβλίων και τεχνικών εγχειριδίων, καθώς και τα αποτελέσματα προσομοιώσεων. Η συνάρτηση \(f(x)\) μπορεί να μας είναι άγνωστη, να μην υπάρχει αναλυτική λύση της ή να είναι πολύ δύσκολος ο υπολογισμός της. Για την εύρεση ενός \(y\) σε τυχαία θέση \(x\) μπορεί να χρησιμοποιηθεί η σειρά των σημείων χρησιμοποιώντας μια μέθοδο παρεμβολής.

Exercise 5.1

Μια μετεωρολογική υπηρεσία ανακοινώνει τις προγνώσεις της με χρονικό βήμα 3 ωρών. Στον Πίνακα 5.1 φαίνεται η πρόβλεψη της θερμοκρασίας για ένα εικοσιτετράωρο. Απεικονίστε την θερμοκρασία σε γράφημα με σημεία (χωρίς γραμμές) και εκτιμήστε την θερμοκρασία στις 05:00 και 20:00.

Table 5.1 Πρόβλεψη θερμοκρασίας.

Πολιτική ώρα [h]	Θερμοκρασία [°C]
0	18
3	16
6	15
9	21
12	25
15	27
18	26
21	23
24	18

import numpy as np
import matplotlib.pyplot as plt

x = np.array([0, 3, 6, 9, 12, 15, 18, 21, 24])
y = np.array([18, 16, 15, 21, 25, 27, 26, 23, 18])

fig, ax = plt.subplots()
ax.set(xlabel='Time [h]', ylabel='Temperature [°C]')

ax.plot(x, y, "o")
plt.xlim(0, 24)
plt.ylim(12, 28)
ax.grid()
plt.show()

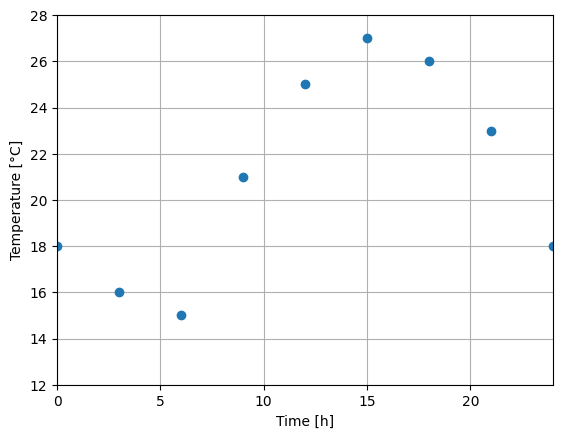
Από το γράφημα φαίνεται ότι στις 05:00 η θερμοκρασία θα είναι περίπου 15.5°C και στις 20:00 24°C.

5.2. Γραμμική παρεμβολή

Η πιο απλή και συνηθισμένη μέθοδος παρεμβολής είναι η γραμμική παρεμβολή κατά την οποία θεωρούμε ότι ευθύγραμμα τμήματα ενώνουν τα γνωστά μας σημεία. Το ευθυγραμμο τμήμα σε καθε διάστημα εκφράζεται μαθηματικά ως:

\[ y=y_i+\frac{y_{i+1}-y_i}{x_{i+1}-x_i}(x-x_i) \;\text{για}\;x_i<x<x_{i+1}\]

Για την επίλυση της Άσκησης 5.1 πρέπει πρώτα να προσδιορίσουμε τα σημεία, τα οποία θα χρησιμοποιήσουμε για τον υπολογισμό.

Για τον υπολογισμό του χρόνου \(x=5\) θα χρησιμοποιήσουμε τα κοντινότερα σημεία, δηλαδή αυτά με \(x_i=3\) και \(x_{i+1}=6\), επομένως:

\[ y= 16+\frac{16-15}{6-3}(5-3)=15.33\]

Ομοίως για \(x=20\) στο αντίστοιχο διάστημα.

import numpy as np
import matplotlib.pyplot as plt

x = np.array([0, 3, 6, 9, 12, 15, 18, 21, 24])
y = np.array([18, 16, 15, 21, 25, 27, 26, 23, 18])

fig, ax = plt.subplots()
ax.set(xlabel='Time [h]', ylabel='Temperature [°C]')

i = 1
xa = 5
ya = y[i]+(y[i+1]-y[i])/(x[i+1]-x[i])*(xa-x[i])
print(xa, ya)

i = 6
xb = 20
yb = y[i]+(y[i+1]-y[i])/(x[i+1]-x[i])*(xb-x[i])
print(xb, yb)

ax.plot(x, y, "o-")
ax.plot([xa, xb], [ya, yb], "rD")   # red diamonds
plt.xlim(0, 24)
plt.ylim(12, 28)
ax.grid()
plt.show()

5 15.333333333333334
20 24.0

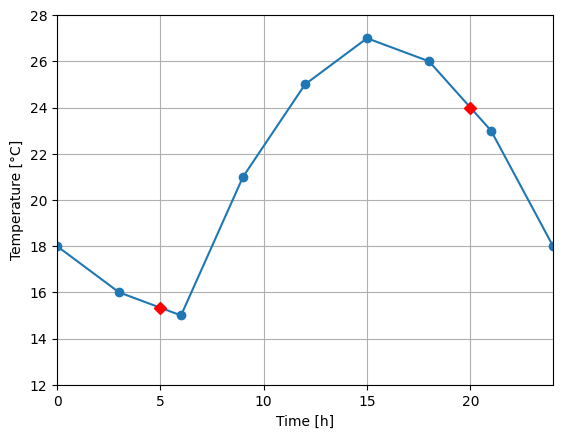
Η γραμμική παρεμβολή δίνει καλά αποτελέσματα όταν η παράσταση ενός μεγεθους προσεγγίζεται ικανοποιητικά από ευθύγραμμα τμήματα. Σε περιπτώσεις με μεγάλη καμπυλότητα απαιτούνται πιο πολλά σημεία για ικανοποιητική ακρίβεια ή μια καλύτερη συνάρτηση παρεμβολής. Η γραμμική παρεμβολή δύναται να εφαρμοστεί και εκτός του διαστήματος των γνωστών σημείων \(x_i\) (extrapolation). Η προσέγγιση αυτή συναντάται με την ονομασία προεκβολή, παρεκβολή ή και παρέκταση. Η προεκβολή πρέπει να χρησιμοποιείται με προσοχή, καθώς η ακρίβειά της μειώνεται μακρυά από τα γνωστά σημεία.

Tip

Η συνάρτηση numpy.interp δέχεται τουλάχιστον τρία ορίσματα, το σημείο της παρεμβολής \(x\) και δύο διανύσματα ίδιου μεγέθους με τα γνωστές σημεία \(x_i\) και \(y_i\). Το διάνυσμα των \(x_i\) πρέπει να έχει αύξουσα σειρά, έτσι ώστε η συνάρτηση να εντοπίσει το κατάλληλο διάστημα \(x_i,x_{i+1}\) που περικλείει το \(x\) της παρεμβολής. Από προεπιλογή η συνάρτηση δεν κάνει προεκβολή, αλλά επιστρέφει την τιμή της \(y_1\) αν \(x<x_1\) και την \(y_n\) αν \(x>x_n\). Το \(x\) μπορεί να είναι κι αυτό διάνυσμα, οπότε κι η συνάρτηση θα επιστρέψει ένα διάνυσμα με τιμές \(y\).

import numpy as np

x = np.array([0, 3, 6, 9, 12, 15, 18, 21, 24])
y = np.array([18, 16, 15, 21, 25, 27, 26, 23, 18])

xa = 5
ya = np.interp(xa, x, y)
print(xa, ya)

xb = 20
yb = np.interp(xb, x, y)
print(xb, yb)

xc = 27
yc = np.interp(xc, x, y)    #no extrapolation
print(xc, yc)

5 15.333333333333334
20 24.0
27 18.0

5.3. Παρεμβολή spline

Στο τελευταίο γράφημα φαίνεται ότι τα ευθύγραμμα τμήματα σχηματίζουν γωνίες μεταξύ τους, οι οποίες φαίνονται πιο καθαρά στις περιοχές που αναμένεται μεγαλύτερη καμπυλότητα. Τα ευθύγραμμα τμήματα δίνουν ασυνεχή πρώτη παράγωγο (κλίση) στα εσωτερικά σημεία, γεγονός μη αναμενόμενο. Για να έχουμε συνέχεια στην πρώτη παράγωγο, πρέπει να παρεμβληθεί πολυώνυμο υψηλότερης τάξης και μάλιστα τρίτου βαθμού για να έχουμε συνέχεια της πρώτης παραγώγου και στα δύο άκρα.

\[ S_i(x) = a_i x^3 + b_i x^2 + c_i x + d_i\;\text{για}\;x_{-1}<x<x_{i} \]

Χρειαζόμαστε εξισώσεις παρεμβολής με τέσσερις άγνωστες παραμέτρους σε \(n-1\) διαστήματα, επομένως πρέπει να καταστρωθεί ένα σύστημα \(4(n-1)\) εξισώσεων.

1. Οι εξισώσεις παρεμβολής πρέπει να δίνουν τις ήδη γνωστές τιμές στα άκρα τους

\[\begin{split} \begin{align} S_i(x_i)&=&y_i& \;\text{για}\;i=0,n-2\;\text{(αριστερό σημείο)}\\ S_i(x_{i+1})&=&y_{i+1}& \;\text{για}\;i=0,n-2\;\text{(δεξιό σημείο)} \end{align} \end{split}\]

\(2(n-1)\) εξισώσεις.

2. Οι συναρτήσεις παρεμβολής από της δύο πλευρές ενός εσωτερικού σημείου πρέπει να έχουν ισοδύναμη πρώτη και δεύτερη παράγωγο

\[\begin{split} \begin{align} S'_i(x_{i})&=&S'_{i+1}(x_{i}) &\;\text{για}\;i=1,n-2\;\text{(πρώτη παράγωγος)}\\ S''_i(x_{i})&=&S''_{i+1}(x_{i}) &\;\text{για}\;i=1,n-2\;\text{(δεύτερη παράγωγος)} \end{align} \end{split}\]

\(2(n-2)\) εξισώσεις.

3. Τέλος επιβάλουμε αυθαίρετα δύο ακόμα περιορισμούς για να οριστεί πλήρως το σύστημα. Μια συνηθισμένη προσέγγιση είναι η μηδενική καμπυλότητα στα ακραία σημεία \(x_i\)

\[\begin{split} \begin{align} S''_1(x_{0})&=&0&\;\text{(πρώτο σημείο)}\\ S''_{n-1}(x_{n-1})&=&0&\;\text{(τελευταίο σημείο)} \end{align} \end{split}\]

2 εξισώσεις.

Tip

Η πλήρης ονομασία της παραπάνω προσέγγισης είναι παρεμβολή με φυσικά κυβικά spline. Είναι διαθέσιμη στην συνάρτηση scipy.interpolate.CubicSpline με την δήλωση ορίσματος bc_type=’natural’.

Exercise 5.2

Λύστε την Άσκηση 5.1 χρησιμοποιώντας φυσικά κυβικά spline (της μονάδας κώδικα SciPy) και σχολιάστε τις διαφορές στην μορφή της καμπύλης στα αποτελέσματα.

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import CubicSpline

x = np.array([ 0,  3,  6,  9, 12, 15, 18, 21, 24])
y = np.array([18, 16, 15, 21, 25, 27, 26, 23, 18])

fig, ax = plt.subplots()
ax.set(xlabel='Time [h]', ylabel='Temperature [°C]')

f = CubicSpline(x, y, bc_type='natural')
xf = np.linspace(0, 24, 24*10)

ax.plot(x, y, "o-")
ax.plot(xf, f(xf), "-")
ax.plot([5, 20], [f(5), f(20)], "rD")   # red Diamonds
plt.xlim(0, 24)
plt.ylim(12, 28)
ax.grid()
plt.show()

print(f(5), f(20))

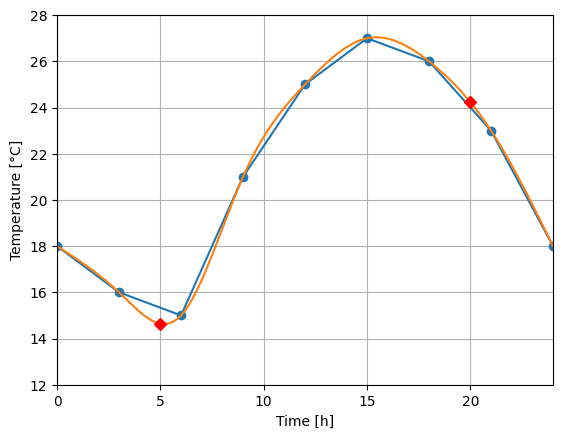
14.647248131784215 24.230036000654557

Παρατηρούμε ότι η διακύμανση της θερμοκρασίας φαίνεται πιο φυσική με χρήση spline. Οι τιμές στις ζητούμενες χρονικές στιγμές διαφοροποιούνται αισθητά από την γραμμική παρεμβολή. Ειδικά στο χρονικό διάστημα 3-6h η γραμμική συνάρτηση δεν ταιριάζει με ρεαλιστική θερμοκρασιακή συμπεριφορά σε αντίθεση με την παρεμβολή spline.

5.4. Παρεμβολή πολυωνύμου

Με δεδομένα \(n\) σημεία οριζεται ένα πολυώνυμο \(n-1\) βαθμού:

\[f(x)=a_0+a_1x+a_2x^2+ \ldots +a_{n-1}x^{n-1} \]

το οποίο έχει \(n\) σταθερούς συντελεστές. Από τα \(n\) γνωστά σημεία προκύπτει ένα γραμμικό σύστημα \(n\) εξισώσεων κατάλληλο για την εύρεση των άγνωστων συντελεστών. Αν και το σύστημα αυτό μπορεί να επιλυθεί με τις μεθόδους που αναφέρθηκαν στο κεφάλαιο 4, η μέθοδος αυτή συνήθως αποφεύγεται. Στην θέση της χρησιμοποιούνται πολυώνυμα ειδικής μορφής που ελαχιστοποιούν τις μαθηματικές πράξεις.

5.4.1. Πολυώνυμα Newton

Τα πολυώνυμα Newton έχουν την μορφή:

\[ f(x) = a_0 + a_1(x-x_0) + a_2(x-x_0)(x-x_1) + \dots + a_{n-1}(x-x_0)(x-x_1)\dots(x-x_{n-1}) \]

ή ισοδύναμα:

\[ f(x) = \sum_{i=0}^{n-1}{a_in_i(x)} \]

όπου:

\[n_i(x) = \prod_{j=0}^{i}(x-x_j)\]

Οι συντελεστές \(a_i\) υπολογίζονται με πεπερασμένες διαφορές:

\[\begin{split} \begin{align} a_0&=&f[x_0]&=&y_0\\ a_1&=&f[x_1,x_0]&=&\frac{f[x_1]-f[x_0]}{x_1-x_0}&=&\frac{y_1-y_0}{x_1-x_0}\\ a_2&=&f[x_2,x_1,x_0]&=&\frac{f[x_2,x_1]-f[x_1,x_0]}{x_1-x_0}&=&\frac{\frac{y_2-y_1}{x_2-x_1}-\frac{y_1-y_0}{x_1-x_0}}{x_2-x_0}\\ \dots&&\dots&&\dots\\ a_i&=&f[x_i,x_{i-1},\dots,x_1,x_0]&=&\frac{f[x_i,\dots,x_1]-f[x_{i-1},x_0]}{x_i-x_0} \end{align} \end{split}\]

Οι πεπερασμένες διαφορές ανώτερης τάξης υπολογίζονται με αυτές της αμέσως προηγούμενης τάξης, επομένως μπορεί να εφαρμοστεί η παρακάτω ακολουθία στήλη προς στήλη:

\[\begin{split} \begin{align} x_0 && \pmb{y_0} \\ && &\rangle & \pmb{f[x_1,x_0]} \\ x_1 && y_1 & & & \rangle & \pmb{f[x_2, x_1,x_0]}\\ && &\rangle &f[x_2,x_1] & & & \rangle & \pmb{f[x_3, x_2, x_1,x_0]}\\ x_2 && y_2 & & & \rangle & f[x_3, x_2,x_1] & & &\rangle & \pmb{f[x_4, x_3, x_2, x_1,x_0]}\\ && &\rangle &f[x_3,x_2] & & & \rangle & f[x_4, x_3, x_2, x_1]\\ x_3 && y_3 & & & \rangle & f[x_4, x_3,x_2]\\ && &\rangle & f[x_4,x_3] \\ x_4 && y_4 \end{align} \end{split}\]

Οι συντελεστές του πολυωνύμου Newton είναι οι κορυφαίες τιμές κάθε στήλης (σημειώνονται με έντονη γραφή). Προσθέτοντας ένα ακόμα σημείο (το \(x_5\) στο παράδειγμα) υπολογίζεται μια γραμμή στην βάση και επεκτείνεται η διάταξη κατά μία στήλη. Έτσι μπορεί εύκολα να μεγαλώσει ο βαθμός του πολυωνύμου παρεμβολής, ένα χρήσιμο χαρακτηριστικό όταν δεν γνωρίζουμε εκ των προτέρων τον επιθυμητό βαθμό.

5.4.2. Πολυώνυμα Lagrange

Το πολυώνυμο Lagrange είναι μια εναλλακτική μέθοδος αναπαράστασης της \(f(x)\), η οποία διευκολύνει κι αυτή τους υπολογισμούς:

\[L(x)=\sum_{i=1}^{i=n} y_i L_i(x) \]

όπου τα γινόμενα \(L_i\):

\[L_i(x)=\prod_{j=1,j\neq i}^{j=n} \frac{x-x_j}{x_i-x_j} \]

Παρατηρείστε ότι παραλείπεται το \(j\) όταν ταυτίζεται με το \(i\). Κάθε γινόμενο \(L_i\) μηδενίζεται στα γνωστά σημεία \(x_i\), εκτός από το \(x_i\) με ίδιο δείκτη στο οποίο παίρνει μοναδιαία τιμή.

H SciPy περιλαμβάνει την σχετική συνάρτηση scipy.interpolate.lagrange.

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import lagrange

x = np.array([ 0,  3,  6,  9, 12, 15, 18, 21, 24])
y = np.array([18, 16, 15, 21, 25, 27, 26, 23, 18])

fig, ax = plt.subplots()
ax.set(xlabel='Time [h]', ylabel='Temperature [°C]')

f = lagrange(x, y)
xf = np.linspace(0, 24, 24*10)

ax.plot(x, y, "o-")
ax.plot(xf, f(xf), "-")
ax.plot([5, 20], [f(5), f(20)], "rD")   # red Diamonds
plt.xlim(0, 24)
plt.ylim(12, 28)
ax.grid()
plt.show()

print(f(5), f(20))

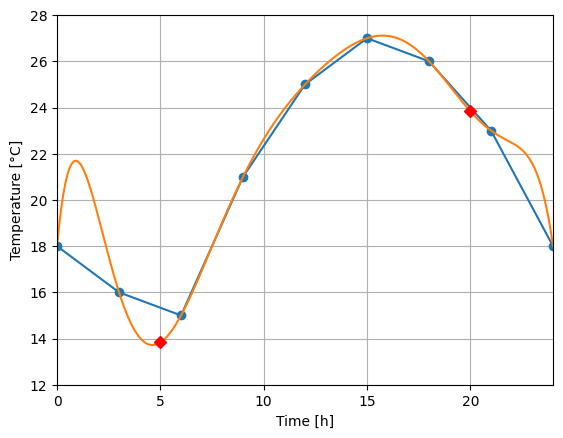
13.830869278058355 23.834527257281152

Tip

Πρέπει να σημειωθεί ότι τα πολυώνυμα ικανοποιούν ακριβώς όλα τα σημεία. Τα πολυώνυμα ανώτερου βαθμού είναι πολύ ευαίσθητα σε σφάλματα που μπορεί να εμπεριέχουν τα δεδομένα μας με συνέπεια να παρουσιάζουν πολλαπλά μέγιστα και ελάχιστα ή γενικώς μη αναμενόμενη συμπεριφορά από φυσικής άποψης. Αυτό συμβαίνει στο διάστημα 0-6 h του παραδείγματος μας. Συνήθως η πιο απλή συμπεριφορά είναι πιο κοντά στην πραγματικότητα.

5.5. Παλινδρόμηση

Όταν τα δεδομένα μας περιέχουν σφάλματα μπορούμε να χρησιμοποιήσουμε μια συνάρτηση \(f(x)\) που δεν περνάει απαραίτητα από τα \(m\) σημεία μας, αλλά αρκετά κοντά. Σε αυτή την περίπτωση δεν κάνουμε παρεμβολή αλλά παλινδρόμηση και η επιλογή της κατάλληλης συνάρτησης γίνεται ακόμα πιο σημαντική. Εδώ θα εξετάσουμε την γενική περίπτωση πολυωνύμου \(n\) βαθμού, η οποία περιλαμβάνει και την γραμμική παλινδρόμηση:

\[f(x)=a_0+a_1x+a_2x^2+ \ldots +a_{n}x^{n} \]

Οι \(n+1\) συντελεστές \(a_j\) πρέπει να επιλεγούν έτσι ώστε να ελαχιστοποιούνται οι αποκλίσεις \(E_i=y_i-f(x_i)\) στα γνωστά σημεία. Η πιο συνηθισμένη προσέγγιση είναι να ελαχιστοποιείται το άθροισμα των τετραγώνων των σφαλμάτων, δηλαδή η μαθηματική έκφραση:

\[S_{r}=\sum_{i=1}^{m} [y_i-f(x_i)]^2=\sum_{i=1}^{m} [y_i-a_0-a_1{x_i}-a_2{x_i}^2- \ldots -a_{n}{x_i}^{n}]^2\]

Το μέγεθος αυτό ελαχιστοποιείται εκεί που οι μερικές παράγωγοί του ως προς \(a_j\) μηδενίζονται, δηλαδή:

\[\begin{split} \begin{align} \frac{\partial S_r}{\partial a_0}&=&-2\sum_{i=1}^{n} [y_i-a_0-a_1{x_i}-a_2{x_i}^2- \ldots -a_{n}{x_i}^{n}]1\\ \frac{\partial S_r}{\partial a_1}&=&-2\sum_{i=1}^{n} [y_i-a_0-a_1{x_i}-a_2{x_i}^2- \ldots -a_{n}{x_i}^{n}]{x_i}\\ \dots\\ \frac{\partial S_r}{\partial a_n}&=&-2\sum_{i=1}^{n} [y_i-a_0-a_1{x_i}-a_2{x_i}^2- \ldots -a_{n}{x_i}^{n}]{x_i}^n \end{align} \end{split}\]

Έτσι προκύπτει ένα γραμμικό σύστημα, το οποίο μπορεί να λυθεί εύκολα.

Η NumPy περιέχει μια ειδική κλάση για τον χειρισμό πολυωνύμων. Για την εύρεση των συντελεστών διατίθεται η μέθοδος fit, η οποία δέχεται ως ορίσματα τα διανύσματα \(x\) και \(y\) και τον βαθμό του πολυωνύμου.

Για την αξιολόγηση της προσέγγισης του πολυωνύμου (αλλά και οποιασδήποτε συνάρτησης παρεμβολής) στα δεδομένα μας χρησιμοποιείται συχνά ο συντελεστής προσδιορισμού (\(R^2\)):

\[R^2=1-\frac{S_{r}}{S_{t}}=1-\frac{\sum_{i=1}^{n} [y_i-f(x_i)]^2}{\sum_{i=1}^{n} [y_i-\bar{y}]^2}\]

Όπως φαίνεται από τον κλάσμα, όταν οι αποκλίσεις τείνουν στο μηδέν, το \(R^2\) τείνει στην μονάδα. Αντιθέτως όταν η συνάρτηση μας είναι το ίδιο καλή με μια μέση τιμή \(\bar{y}\), δηλαδή δεν εξηγεί καθόλου την εξάρτηση από το \(x\), το \(R^2\) τείνει στο 0.

import numpy as np
import matplotlib.pyplot as plt
from numpy.polynomial import Polynomial

x = np.array([ 0,  3,  6,  9, 12, 15, 18, 21, 24])
y = np.array([18, 16, 15, 21, 25, 27, 26, 23, 18])

fig, ax = plt.subplots()
ax.set(xlabel='Time [h]', ylabel='Temperature [°C]')

f = Polynomial.fit(x, y,deg=5)
xf = np.linspace(0, 24, 24*10)

Rsq=np.corrcoef(y,f(x))[0,1]**2 # Calculation of R2 from Pearson correlation matrix.

print(Rsq)

ax.plot(x, y, "o-")
ax.plot(xf, f(xf), "-")
ax.plot([5, 20], [f(5), f(20)], "rD")   # red diamonds
plt.xlim(0, 24)
plt.ylim(12, 28)
plt.text(20, 27, f'R²={Rsq:0.1%}')

ax.grid()
plt.show()

print(f(5), f(20))

0.9771452505827505

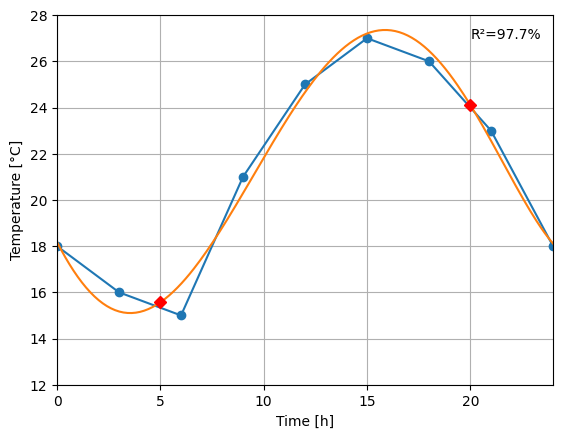
15.568138651471992 24.10774410774413